Algebraic Terms Definition
Section 1
Number Theory : Branch of mathematics concerned with
numbers used for counting.
Natural Numbers: N : counting numbers: {1, 2,3, 4,...}
Factors: Natural numbers multiplied together to get a product
Divisible: if when division occurs the remainder is 0.
b|a : a is divisible by b, b is a divisor of a, and b divides a
Prime Number: N > 1 such that only 1 and itself are factors.
Composite Number: N >1 such that it is divisible by a number other than 1 and
itself.
Prime Factorization: Expressing a composite number as a product of primes.
Fundamental Theorem of Arithmetic: Every composite number can have only one
result
for its prime factorization.
Relatively Prime: Pairs of numbers such that the only factor that have in common
is 1,
GCF = 1.
Find Greatest Common Factor: (GCF)
1. Write each number as product of prime
2. Find common primes in all numbers concerned
3. Multiple the common primes together
Least Common Multiple: LCM (Least Common Divisor): smallest natural number that
is
divisible to each number in question.
How to find the LCM
1. Write each number as product pf primes
2. Start with largest number and see what is missing from the others
3. Multiply missing numbers to the largest number
LCM → Common denominator.
Section 2
Whole Numbers: {0,1, 2,3, 4,....}
Integers: {...− 4,−3,−2,−1,0,1, 2,3, 4,...}
*** Zero is neither positive or negative
Inequality : < or >; ≤ or ≥
Absolute Value: distance to zero. Absolute value of any integer is positive.
Adding : Sum
Additive Inverse: Sum = 0; opposites
Subtraction: Difference
Multiplication: Product
Quotient: Result of division
| Please | ( ) – grouping |
| Excuse | Exponents |
| My Dear | Multiply / Divide |
| Aunt Sally | Add / Subtract |
Section 3
Rational Numbers: can be written as a fraction
Fundamental Principle of Rational Numbers
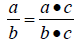
Mixed Number: 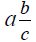 , sum of
an integer and a rational number.
, sum of
an integer and a rational number.
Improper Fraction: numerator > denominator
Convert Mixed to Improper
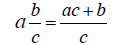
Convert Improper to Mixed
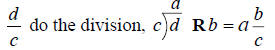
Terminating Decimal: decimal that stops
Repeating Decimal: Decimal where digits repeat indefinitely
How to express repeating decimal as fraction
1. Set n = number of digits repeating
2. Count number of digits repeating, and multiply by that power of 10.
3. Subtract equation from #1 from equation in #2.
4. Solve for n.
Reciprocal : multiplicative inverse: flip the fraction; product of a number and
its
reciprocal = 1.
*** Fractions must have common denominators to add or subtract with them.
Density of Rational Number: There will always be some rational number that can
be
found between any two rational numbers.
Section 4
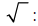 radical sign
radical sign
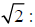 radical and 2 is a
radicand.
radical and 2 is a
radicand.
Irrational Number: number whose decimal representation is
nether termination or
repeating. Cannot be written as a fraction.
Principal Square Root : 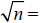 positive number that when multiplied by itself the result is
positive number that when multiplied by itself the result is
n.
*** not all square roots are irrational
Product Rule:
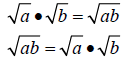
Quotient Rule:
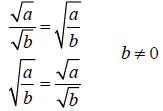
Rationalize the denominator: Multiply both numerator and
denominator by the smallest
number to produce a perfect square in the denominator.
Section 5
Real Numbers: Union of rational and irrational numbers.
Properties of Real Numbers
Closure: When performing an operation the type of number you put in, your result
is the same type of number.
Associative: (a + b) + c = a + (b + c)
Commutative: a + b = b + a; ab = ba
Distributive: a(b + c) = ab + ac
Section 6
Properties of Exponents
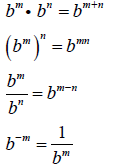
Powers of Ten
Positive exponent → move decimal to right same number of digits as zeros.
Negative exponent → move decimal to left same number of digits as zeros.
**For both add filler zeroes.
Scientific Notation:
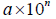 n is an integer ; 1≤ a
<10
n is an integer ; 1≤ a
<10
Convert from Decimal to Scientific Notation
If n is positive, move n decimals to right, add filler zeros.
If n is negative, move n decimals to left, add filler zeroes.
Convert from Scientific Notation to Decimal
1. Move decimal till you get a number between 1 and 10
2. Number of places is n
3. If original number is < 1 → n is negative,
if original number is > 10 → n is positive.
Computations with Scientific Notation
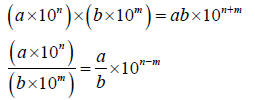
Section 7
Arithmetic Sequence: sequence that each term after the first differs by a
constant number,
we can this constant difference d .
General term: 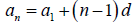
Geometric Sequence: sequence that each term after the
first is obtained by multiplying
the previous term by a common ratio we refer to as r.
General term: 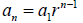
| Prev | Next |