Algebra of Matrices Systems of Linear Equations
ALFONSO SORRENTINO
[Read also § 1.1-7, 2.2,4, 4.1-4]
1. Algebra of Matrices
Definition. Let m, n be two positive integers. A m by n real matrix is an
ordered
set of mn elements, placed on m rows and n columns:
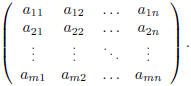
We will denote by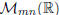 
the
set of m by n real matrices . Obviously, the set
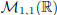can be identified with R (set of real
numbers).
NOTATION:
Let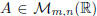 
. To simplify the notation , sometimes we
will abbreviate A =
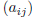. The element
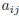is placed on the i-th row and j-th column,
it will be also
denoted by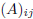 
. Morerover, we will denote by
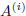the i-th row
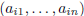of
A and by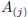 
the j-th column 
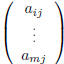of A. Therefore:
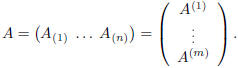
Remark. For any integer n ≥1, we can consider
the cartesian product Rn. Obviously,
there exists a bijection between Rn and 
or
.
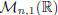Definition. Let .
The transpose of A is a matrix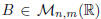 
such that:
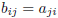for any i = 1, . . . , n and j = 1, . .
. , m.
The matrix B will be denoted by AT . In few words, the i-th row of A is simply
the
i-th column of AT :
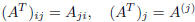and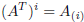 
.
Moreover,
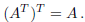
We will see that the space of matrices can be endowed with
a structure of vector
space. Let us start, by defining two operations in the set of matrices
:
the
addition and the scalar multiplication.
• Addition:
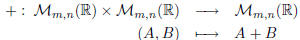
where A + B is such that:
.
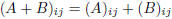• Scalar multiplication:
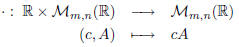
where cA is such that: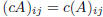 
.
Proposition 1. (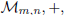
, ·) is a vector space. Moreover its dimension is mn.
Proof. First of all, let us observe that the zero vector is the zero matrix 0
[i.e., the
matrix with all entries equal to zero: 0ij = 0]; the opposite element (with
respect
to the addition) of a matrix A, will be a matrix −A, such that
.
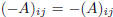We leave to the reader to complete the exercise of verifying that all the axioms
that
define a vector space hold in this setting.
Let us compute its dimension. It suffices to determine a basis. Let us consider
the
following mn matrices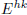 
(for h = 1, . . . ,m and k = 1, . . . , n), such that:
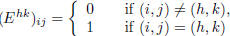
[in other words, the only non- zero element of
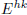is the
one on the h-th row and
k-th column]. It is easy to verify that for any
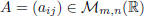, we have:
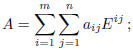
therefore this set of mn matrices is a spanning set of . Let us verify that
they are also linearly independent . In fact, if
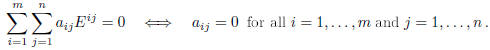
This shows that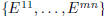 
is a basis.
Definition. Let .
• A is a square matrix (of order n), if m = n; the n-ple
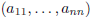is
called
diagonal of A. The set will be simply denoted by
.
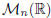• A square matrix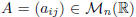 
is said upper triangular [resp. lower
triangular] if aij = 0, for all i > j [resp. if aij = 0, for all i < j].
• A square matrix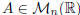 
is called diagonal if it is both upper and lower
triangular [i.e., the only non-zero elements are on the diagonal: aij = 0,
for all i ≠ j].
• A diagonal matrix is called scalar, if
.
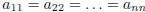• The scalar matrix with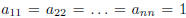 
is called unit matrix,
and will be denoted In.
• A square matrix 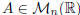is symmetric if A = AT [therefore, aij = aji]
and it is skew-symmetric if A = −AT [therefore, aij = −aji].
Now we come to an important question: how do we multiply two matrices ?
The first step is defining the product between a row and a column vector.
Definition. Let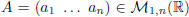 
and
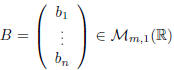. We
define the multiplication between A and B by:
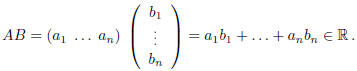
More generally, if
and
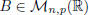, we define the
matrix product :
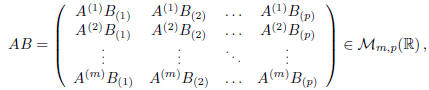
where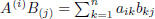 
, for all i = 1, . . . ,m and j = 1, . . . , p.
Remark. Observe that this product makes sense only if the number of columns of
A is the same as the number of rows of B. Obviously, the product is always
defined
when the two matrices A and B are square and have the same order.
Let us see some properties of these operations (the proof of which, is left as
an
exercise).
Proposition 2. [Exercise]
i) The matrix multiplication is associative; namely:
(AB)C = A(BC)
for any ,
and
.
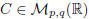ii) The following properties hold:
(A + B)C = AC + BC, for any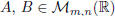 
and
;
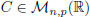A(B + C) = AB + AC, for any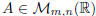 
and
;
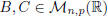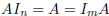, for any
;
(cA)B = c(AB), for any c ∈ R and
,;
(A + B)T = AT + BT , for any ;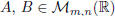
(AB)T = BTAT , for any and
.
Remark. Given a square matrix
, it is not true in general that there
exists a matrix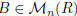 
such that AB = BA = In. In case it does, we say that
A is invertible and we denote its inverse by A-1.
Let us consider in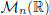 
the subset of invertible matrices:
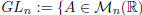: there exists 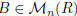such that AB = BA = In} .
This set is called general linear group of order n.
We leave as an exercise to the reader, to verify that the following properties
hold.
Proposition 3. [Exercise]
i) For any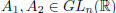 
, we have:
.
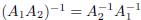ii) For any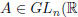 
, we have:
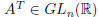and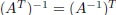 
.
iii) For any 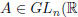and c ∈ R, with c ≠ 0,
we have: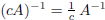 
. In
particular,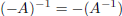 
.
An important subset of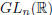 
, that we will use later on, is the set of
orthogonal
matrices.
Definition. A matrix
is called orthogonal, if:
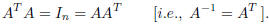
The set of the orthogonal matrices of order n is denoted
by On(R). Moreover,
from what observed above (i.e., A-1 = AT ), it follows that
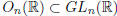(i.e.,
orthogonal matrices are invertible).
To conclude this section, let us work out a simple exercise, that will provide
us with
a characterization of O2(R).
Example. The set O2(R) consists of all matrices of the form:
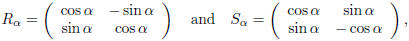
for all α ∈ R.
Proof. One can easily verify (with a direct computation), that:
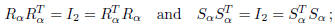
therefore, these matrices are orthogonal. We need to show
that all orthogonal
matrices are of this form.
Consider a matrix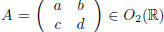 
. Let us show that there
exists α ∈ R,
such that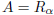 
or
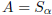. By Definition:
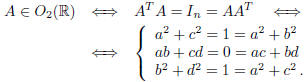
From the first two equations , if follows that b2 = c2. There are two cases:
i) b = c or ii) b = −c .
i) In this case, plugging into the other equations, one gets that (a + d)c = 0
and therefore:
i') c = 0 or i'') a + d = 0 .
In the case i'):
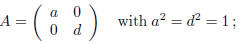
namely, A is one of the following matrices:
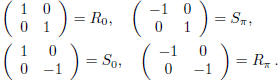
In the case i ):
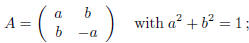
therefore,
with α∈ [0, 2π ) such that (a, b) = (cos2α,
sin2α) (this
is possible since a2 + b2 = 1).
ii) Proceeding as above, we get that (a − d)c = 0 and
therefore there are two
possibilities:
ii') c = 0 or ii'') a − d = 0 .
In the case ii'), we obtain again:
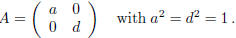
In the case ii ):
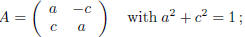
therefore,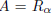 
with α∈ [0, 2π ) such that (a, c) = (cos2α,
sin2α) (this
is possible since a2 + c2 = 1).
| Prev | Next |