A Quick Guide to Recognizing Linear,Quadratic,and Exponential Functions

A Quick Guide to Recognizing Linear, Quadratic, and Exponential Functions

1. Tables
Important Note: The Input Values MUST be equally spaced

Linear Function	Quadratic Function	Exponential Function
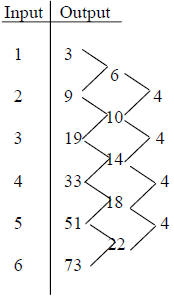
Output difference is constant	First difference is linear Second difference is constant	Output ratios are constant

2. Explicit Equations

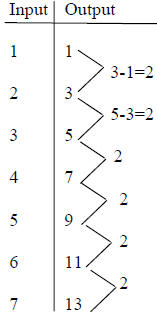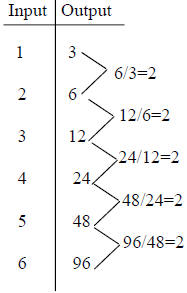Important note: There are many different forms of both the explicit and recursive equations for
the same function.

Linear: Terms are constants or constant times a variable. Examples: y = mx + b ,
2· (H -1) = T , y - 3 = 7x + 8, and Output = 2 x Input -1.

Quadratic: Terms include constant times the square of the input variable and can also include
linear terms as above. Examples: Area = (side)², y = ax² + bx + c , and

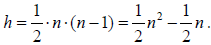
Exponential: A constant times a base raised to a variable exponent. Examples: y = 2^x ,
K = 3·2^P , Balance = 1000 x (1.005)^months.

To Commentary Doc File PDF File Home

3. Recursive Equations

Linear: Initial Row = ____ (fill in blank with a number); Next Row = Previous Row + ___
(fill in blank with a number )

Example: In the first table, the initial output value is 1, and we add 2 to get the next value.
More formally: f (1) =1, f (n +1) = f (n) + 2

Quadratic: Initial Row = ____ (fill in blank with a number); Next Row = Previous Row + ___
(fill in blank with a linear function )

Example: In the second table on the other page, the output value in the initial row is 3, and we
add 4 x (Input) +2 to get the next value. More formally: f (1) = 3, f (n +1) = f (n) + 4n + 2

Exponential: Initial Row = ____ (fill in blank with a number); Next Row = Previous Row x ___
(fill in blank with a number )

Example: In the third table on the other page, the output value in the initial row is 3, and we
multiply by 2 to get the next value. More formally: f (1) = 3, f (n +1) = 2· f (n) .

4. Graphs

Note 1: You cannot tell for sure whether a function is quadratic or exponential just from
the graph. There are other functions whose graphs look like quadratics and exponentials.

Note 2: Be careful if the domain (possible input values) is restricted. For example, in many
physical problems, it makes no sense to include negative inputs , but this restriction takes away
some of the information that might help you identify the shape of the graph.

Linear: A straight line

Quadratic: A parabola. Has a maximum or a minimum, and is symmetric about a vertical axis.
Often looks “U Shaped,” but can be deceptive; for example, if small portions are magnified they
can look like straight lines.

Examples on next page

Exponential: Either grows or decays at a rate proportional to the function, so eventually either
starts growing very quickly or shrinking to zero very quickly.

Examples on next page

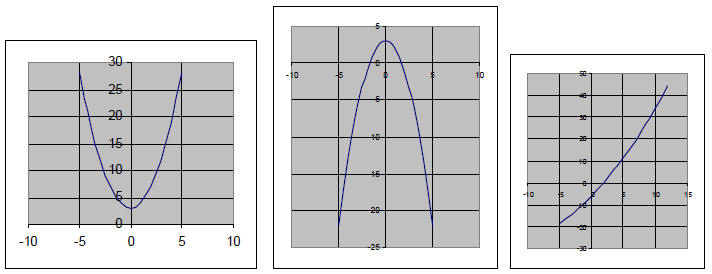
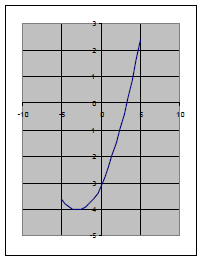
Examples of Quadratic Functions

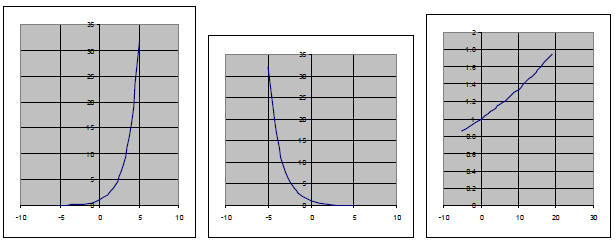
Examples of Exponential Functions (note the last one hasn’t “taken off” yet; note similarities with
the third quadratic function).