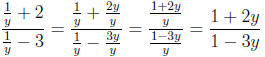Math 105 Exam II Solution
2. Divide. (10)
(3x4 - 5x3 + 4x2 - 5x + 1)  (x2 + 1)
(x2 + 1)
Solution :
We cannot use synthetic division since the divisor is not of the form x-a. We
use long
division instead after rewriting the divisor as x2 + 0x + 1. We
obtain 3x2 - 5x + 1.
3. Use the remainder theorem to find f(4), where f(x) = x4 -x3
- 19x2 + 49x - 30. (10)
Solution:
Use 4 for the synthetic division .
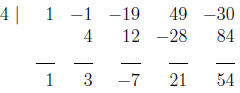
So f(4) = 54.
4. Solve the equation 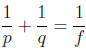 for p (10)
for p (10)
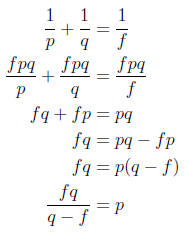
5. Simplify. (10)
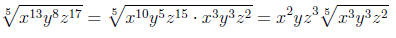
Since the root is odd , we need no absolute values.
6. Divide and simplify . (10)
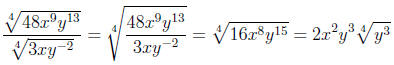
Since both x and y appear with odd powers under the
radical in the original ex-
pression , they both had to be positive in the first place. Therefore, the final
expression
needs no absolute value.
7. Factor completely .(10)
x2(x + 3) - 4(x + 3) = (x + 3)(x2 - 4) = (x + 3)(x + 2)(x
- 2)
8. Determine the domain of f. (10)
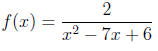
The domain of f is the set of values x ∈ R for which the
denominator x2-7x+6 is not
equal to 0. To obtain the values that must be excluded from R, set the
denominator
equal to zero :
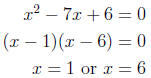
The domain of f is therefore {x ∈ R l x≠ 1, x ≠ 6}.
9. Divide and, if possible, simplify. (10)
Solution:
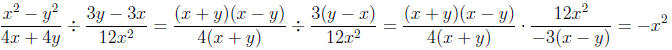
10. Find the LCD , then add and simplify. (10)
Solution:
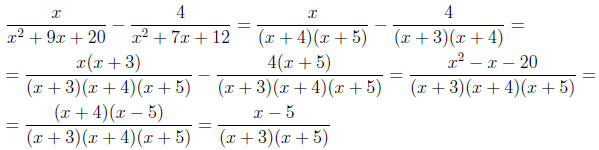
11. Rosanna walks 2 mph slower than Simone. In the time it
takes Simone to walk 8 mi,
Rosanna walks 5 mi. Find the speed of each person. (10)
Solution:
| d | r | t | |
| Rosanna | 5 | x - 2 | t |
| Simone | 8 | x | t |
Since d = r . t, we have t
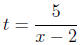
and 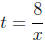 .Setting the equations equal we get
.Setting the equations equal we get
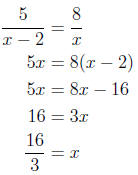
Simone walks at a rate of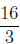 mph
and Rosanna at a rate of
mph
and Rosanna at a rate of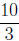 mph.
mph.
| Prev | Next |