Worksheet 6 Polynomials

Move everything to one side. Factor . Expand. Complete the square!
xⁿ − yⁿ =?, x^2m+1 + y^2m+1 =?. A degree n polynomial is determined
by its values at n + 1 points. Coefficients of a polynomial in terms of
its roots. How to get sums of powers of roots ? Rational roots theorem
(if a polynomial with integer coefficients has a rational root then ???).
Long division of polynomials .

1. 1/(x + 1)(x + 2)(x + 3) =?/(x + 1)+?/(x + 2)+?/(x + 3).

2. Consider two polynomials, P(x) and Q(x). Suppose that each of
them has the property that the sum of its coefficients at odd powers
of x is equal to the sum of its coefficients at even powers of x . For
example, we can take P(x) = 1+3x+2x² and Q(x) = −1+4x² +3x³.
Is it true that P(x)Q(x) has the same property?

3. Show that each number in the sequence 49, 4489, 444889, 44448889,
... is a perfect square .

4. Find the remainder when you divide x⁸¹ + x⁴⁹ + x²⁵ + x⁹ + x by
x³ − x.

5. If P(x) is a polynomial of degree n such that P(k) = k/(k + 1)
for k = 0, . . . , n, determine P(n + 1).

6. Prove that 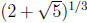is irrational but
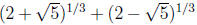
is rational .

7. It is known that a quadratic equation has either 0, 1, or 2 unique
real solutions . But consider the equation


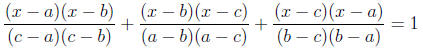
where a, b, and c are distinct. Notice that x = a, x = b, and x = c are
all solutions — how can this equation have three solutions?

8. (The interpolation formula) Suppose a₁, ..., a_n are distinct num-
bers, and b₁, ..., b_n are given numbers, and P(x) is a degree at most
n − 1 polynomial such that P(a_i) = b_i for all i. Show that


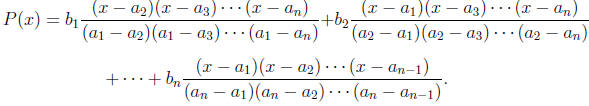
9. A repunit is a positive integer whose digits in base 10 are all ones.
Find all polynomials f with real coefficients such that if n is a repunit,
then so is f(n).

10. Solve
(x² − 3x − 4)(x² − 5x + 6)(x² + 2x) + 30 = 0.

11. Let k be a positive integer. Prove that there exist polynomials
P₀(n), P₁(n), . . . , P_k-1(n) (which may depend on k) such that for any
integer n,

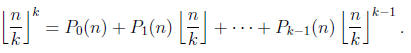
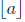( means the largest integer ≤ a.)