Topic 13 - Polynomial Functions
Symmetry
• A polynomial function with all even exponents is an even function and
symmetric about the y-axis.
• A polynomial function with all odd exponents is an odd function and symmetric
about the origin.
• A quadratic function is symmetric about its axis of symmetry x = −b/2a .
x-Intercepts
The roots of a polynomial function correspond to the
x- intercepts of its graph.
• If a root has odd multiplicity , the graph crosses the x-axis at the
corresponding x-intercept.
• If a root has even multiplicity , the graph touches but does not cross the
x-axis at the corresponding x-intercept.
Consider the polynomial 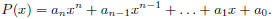
• For n odd and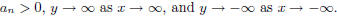
• For n odd and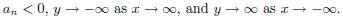
• For n odd and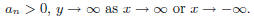
• For n odd and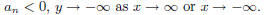
Strategy for Graphing Polynomial Functions
1. Check for symmetry.
2. Find the x- intercepts and the y -intercept.
3. Determine the behavior of the graph at the x-intercepts.
4. Determine the behavior of the graph as 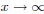 and
as
and
as 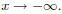
5. Calculate ordered pairs if necessary.
6. Draw a smooth curve connecting the points.
Example 1
Graph the polynomial function f(x) = x^3 − 7x + 6.
1. This is not an even, odd, or quadratic function . The
graph has no symmetry.
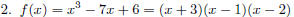
The x- intercepts are (−3, 0), (1, 0), and (2, 0).
The y-intercept is (0, 6).
3. The graph crosses the x-axis at each x-intercept.
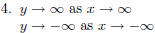
5. f(−2) = (−2)^3 − 7(−2) + 6 = 12
The ordered pair (−2, 12) is a point on the graph.
Example 2
Graph the polynomial function g (x) = −x^3 + 9x.
1. This is an odd function. The graph is symmetric about the origin.
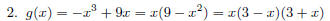
The x-intercepts are (−3, 0), (0, 0), and (3, 0).
The y-intercept is (0, 0).
3. The graph crosses the x-axis at each x-intercept.
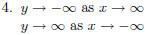
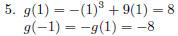
The ordered pairs (1, 8) and (−1,−8) are points on the graph.
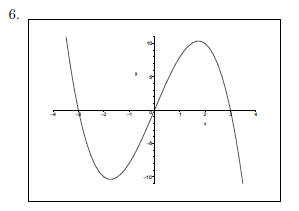
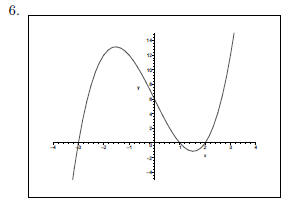
Example 3
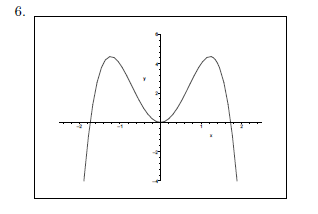
Graph the polynomial function h (x) = −2x^4 + 6x^2.
1. This is an even function. The graph is symmetric about the y-axis.
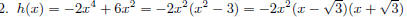
The x-intercepts are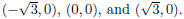
The y-intercept is (0, 0).
3. The graph crosses the x-axis at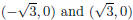
The graph touches but does not cross the x-axis at (0, 0).
5. h(1) = −2 + 6 = 4
h(−1) = h(1) = 4
The ordered pairs (1, 4) and (−1, 4) are points on the graph.
| Prev | Next |