Basics of Programming. TI-83 Programming

You can think of a program as of a machine which produces the result (OUTPUT)
based on the data you entered (INPUT).

Examples of the simplest programs are those that handle the input using a single
formula and then produce an output.

Examples:
1. Quadratic formula. Input: coefficients a, b, and c: Output: solutions x₁ and x₂ if
they exist, or an error message if they do not. For example, on your TI83, this
would be

PROGRAM:QUADFORM
: Input A
: Input B
: Input C

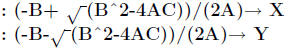
: Disp X, Y

2. Scalar Product of vectors . Input: the coordinates of two vectors (a, b, c) and (d, e, f).
Output: the scalar product s:

PROGRAM: DOT
: Input A
: Input B
: Input C
: Input D
: Input E
: Input F
: A*D+B*E+C*F → S
: Disp S

The following is a "user friendly" version of the above QUADFORM program.

PROGRAM:QUADFORM
: Disp "ENTER A"
: Input A
: Disp "ENTER B"
: Input B
: Disp "ENTER C"
: Input C

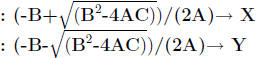
: Disp " SOLUTIONS ARE ", X, Y

Branching

In most cases, the programs cannot be reduced to a simple application of a single
formula.

Let us consider the above program for solving an quadratic equation again. If the
solutions are not real, the error message will appear and the program will have to be
terminated. A much better program for solving a quadratic equation would be the one
that would not require the brute force termination of the program in case of complex
solutions. The idea for improvement is to use the following reasoning:

IF the solutions are not real, THEN display the message that there is no real
solutions (without using the quadratic formula) and GO TO the end of the program;

ELSE calculate and display the solutions.

This idea is implemented as follows

: PROGRAM:QUADFORM
: Disp "ENTER A"
: Input A
: Disp "ENTER B"
: Input B
: Disp "ENTER C"
: Input C
: B^2-4AC → D
: If D< 0
: Then
: Disp "NO REAL SOLUTIONS "
: Goto 1
: Else

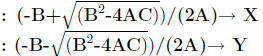
: Disp "SOLUTIONS", X, Y
: Lbl 1

This is an example of a program where a decision making is involved: in certain case
one sequence of commands is performed, in certain other cases the other sequence of
commands is performed. This is called branching. The simplest type of branching is
with commands IF, THEN, ELSE just like in the above example.

Loops

Another situation that frequently appears in programming is when a sequence of
commands should be repeated several times. For example, to find a sum of the series

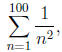
one would not add 100 numbers by hand . The basic idea involves recursive reasoning:
keep adding 1/n² term at each step to the sum computed at previous step. This give us
the following informal idea for a program:

At the first step, sum is 1.

FOR all n's between 1 and 100, if the sum is equal to s after less than n steps, after
n steps it will be s + 1/n².

On your TI83, this can be implemented as follows.

PROGRAM: EASYSUM
: 0 → S
: For (N, 1, 100)
: S + 1/N^2 → S
: End
: Disp "SUM IS", S

Let us consider a bit more complex situation . Suppose now that we need to sum the
series

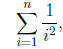
for any given n: In this case the number of terms, n; needs to be entered as an input of
the program. This gives us,

PROGRAM: SUM
: Disp "ENTER NUMBER OF TERMS"
: Input N
: 0 → S
: For (I, 1, N)
: S + 1/I^2 → S
: End
: Disp "SUM IS", S

Yet a more complex situation is when we need to find the first few decimals of the
(convergent) sum

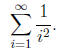
For example, suppose that we need to calculate exactly the first few decimals of this sum.
Here we cannot use the FOR loop since we do not know how many terms we need to add
in order to obtain the required accuracy. The informal idea is the following

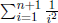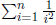WHILE the difference D of and is greater than given small number,
keep increasing the number of terms n.

When D becomes smaller than the given small number, approximate 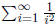with

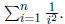
PROGRAM: SUM2
: Disp "ENTER SMALL NUMBER"
: Input E
: 1 → N
: 0 → P
: P+1 → S
: While abs(S-P) ≥ E
: N+1 → N
: S ! P
: P+1/N^2 → S
: End
: Disp "SUM IS", S
: Disp "NUMBER OF STEPS NEEDED IS", N

Further Examples

To write an algorithm for computing the factoriel of a given integer, it is helpful to
think of factoriel function

n ! = 1 times 2 times 3 times ... times n

as of recursive sequence:

Factoriel(1) = 1.

Factoriel(n) = Factoriel(n - 1) times n:

This idea transfers to the following TI83 program:

PROGRAM: FACTORL1
: Disp "ENTER N"
: Input N
: 1 → F
: For (I, 1, N)
: F * I → F
: End
: Disp "N FACTORIEL IS", F

Here we use the FOR loop. The following illustrates the use of WHILE loop for
computing the same factoriel function for given n.

PROGRAM: FACTORL2
: Disp "ENTER N"
: Input N
: 1 → F
: 1 → I
: While I ≤ N
: F * I → F
: I+1 → I
: End
: Disp "N FACTORIEL IS", F

Although the use of WHILE loop seemed longer in this example, sometimes it is
necessary to use WHILE as the FOR loop cannot be used. The program SUM2 is an
example of this situation.

To approximate the integral

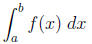
the left sum of function f(x) on interval [a, b] with n subintervals can be considered. In
this case, we are adding the areas of rectangles of height f(x_i) for i = 0,… n - 1 and of
the width h = (b - a)/n.

L(n) = h times f(x₀) + h times f(x₁) + ... + h times f(x_n-1).

In order to write a program, it is again useful to think of the above formula for L in
a recursive form:

L(0) = 0,
L(i + 1) = L(i) + h times f(x_i).

PROGRAM: LEFTSUM (Prior to execution of the program, enter f(x) in Y1= on
your TI83.)
: Disp "LOWER BOUND"
: Input A
: Disp "UPPER BOUND"
: Input B
: Disp "NUMBER OF SUBINTERVALS"
: Input N
: 0 → L
: (B-A)/N → H
: For (I, 0, N-1) (The only di erence for the right sum would be this line .)
: A+H_i → X (Place xi value in variable X.)
: L+H*Y1 → L (Y1 is the f- value of x . So, at i-th step, this is f(x_i).)
: End
: Disp "LEFT SUM", L

Practice Problems:

1. Write down a program that will calculate the polar coordinates (r,θ ) of the given
point in Cartesian coordinates (x; y):

2. Write a program that calculates the absolute value of a given number.

3. The number π can be calculated using the following formula:

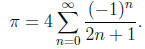
Write programs that:

a) Approximates π with the first 1000 terms of the above sum.
b) Approximates π with the first n terms of the above sum, for given n:
c) Approximates π using the above sum to three decimals.

4. Consider the following recursive sequence

a(0) = 0;

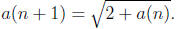
To check if this sequence is convergent, we might calculate the terms and monitor
how close they are to one another as n is increasing. If they are getting closer and
closer to one another as n is getting larger, the sequence is convergent and the limit
is the number to which the terms are approaching. Note that we cannot use the
FOR loop since we are not given n in advance.

Using an idea similar to the one in SUM2, write a program that computes the limit
of the above sequence to three decimal places.

5. For a given n, calculate the n-th term of the sequence

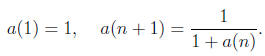
Use that program to try to figure out the convergence.

6. What will change in the program LEFTSUM if the program needs to calculate the
Right, Mid, Trapezoidal or Simpson's Sum?