Intermediate Algebra Review Notes Exam #4
Exercise 6(a) To place f(x) = x2 -6x-10 in vertex form,
take one-half of the middle coefficient
and square, i.e., [(1/2)(-6)] = 9. Add and subtract this amount , factor and
simplify .
f(x) = x2 - 6x + 9 - 9 - 10
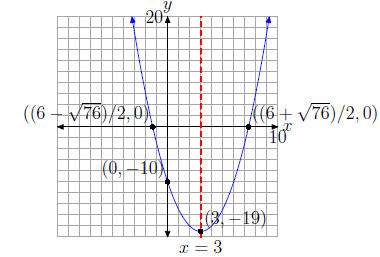
f(x) = (x - 3)2 - 19
The parabola opens upward, the vertex is at (3,-19), and the equation of the
axis of symmetry is
x = 3.
Because f(0) = -10, the y- intercept is (0,-10). To find the x-intercept, set y =
0.
0 = x2 - 6x - 10
Note that ac = (1)(-10) = -10. There is no integer pair that has product -10 and
sums to -6.
Hence, we will need to use the quadratic formula .
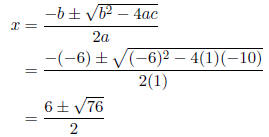
Thus, the x-intercepts are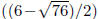
and
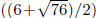. Using a calculator , these approximately
equal -1.35 and 7.35.
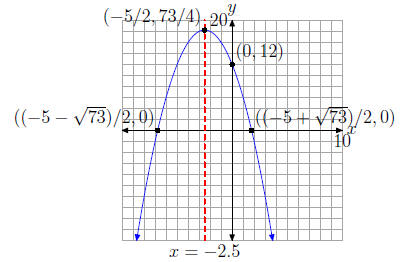
Exercise 6(b) To place f(x) = -x2 - 5x + 12 in vertex
form, first factor out a -1.
f(x) = - [
x2 + 5x - 12 ]
Take one-half of the middle coefficient and square , i.e., [(1/2)(5)] = 25/4. Add
and subtract this
amount, factor and simplify .
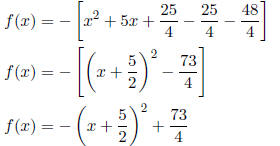
The parabola opens downward, the vertex is at (-5/2,
73/4), and the equation of the axis of
symmetry is x = -5/2.
Because f(0) = 12, the y-intercept is (0, 12). To find the x-intercept, set y = 0,
then multiply
both sides of the equation by -1.
0 = -x2 - 5x + 12
0 = x2 + 5x - 12
Note that ac = (1)(-12) = -12. There is no integer pair that has product -12 and
sums to 5.
Hence, we will need to use the quadratic formula .
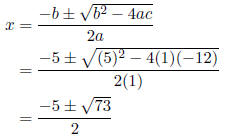
Thus, the x-intercepts are
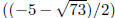and 
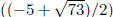. Using a calculator, these approxi-
mately equal -6.7720 and 1.7720.
Exercise 7. Let x and y represent numbers. Their difference
is 12, so
x - y = 12. 
(1)
The sum of their squares is
S = x2 + y2. (2)
Solve equation (1) for x.
x = y + 12 (3)
Substitute equation (3) into equation (2), expand and simplify.
S = (y + 12)2 + y2
S = y2 + 24y + 144 + y2
S = 2y2 + 24y + 144
This is a parabola that opens upward, so the minimum S- value will occur at the
vertex. The
y-value of the vertex is given by
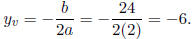
To find the second number, substitute y = -6 in equation
(3).
x = -6 + 12
x = 6
Thus, the numbers are x = 6 and y = -6.
Exercise 7
Exercise 8. One number is 5 less than twice a second number. So, the numbers are
2x-5 and x.
The product of the two numbers is given by
P = (2x - 5)x
P = 2x2 - 5x.
This is a parabola that opens upward, so P will have a minimum at the vertex of
the parabola.
The x-value of the vertex is given by
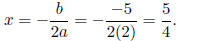
The first number is
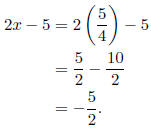
Hence, the two numbers are 5/4 and -5/2.
Solutions to Multiple Choice Questions
Solution to Question 1: -3
Solution to Question 2: 1
Solution to Question 3: -x + 1
Solution to Question 4: 2x
Solution to Question 5: (-7, 7)
Solution to Question 6: (-∞,-7] ∪ ∪7,∞)
Solution to Question 7: No solutions
Solution to Question 8: x = 2
Solution to Question 9: (1/4,-9/8)
Solution to Question 10: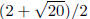 
Solution to Question 11: None of these. The correct solution is k = -25/24.
Solution to Question 12: 7
Solution to Question 13: 1.5
| Prev | Next |