Applications of Linear Equations
General Steps For Solving Word Problems
1. Read the problem through at least once to familiarize yourself with the
situation (don’t
worry about any details).
2. Decide what it is you are being asked to find (usually the last sentence and
it has a question
mark). This is usually the best choice for the “unknown”.
3. Write down “let x = the thing I’m trying to find”
4. Now, read that problem again. This time, pay attention to the details. Find
some way of
organizing those details (a list of expressions , a picture, a chart, a table,
whatever works).
5. Read that problem again and look at your details. You need to write an
EQUATION that
relates some of those details to the others. Look for something that is equal to
something
else. Use your common sense , knowledge of the situation, and/or geometry
formulas to find
an equation .
6. Write the equation and solve for the unknown .
7. Answer the question that was asked with a sentence.
8. Check your answer by placing your answer in the original situation and seeing
if it works.
DON’T check your answer by plugging it back into your equation! If you’ve made a
mistake, it’s most likely the equation itself that is wrong.
Example:
If you double a number and then add 85, you get 3/4 of the original number. What
is the original
number?
Let x = the original number
In reading this problem, notice that it says basically if you do some stuff to
the original number you get
something. You get means equals!
If you double a number and then add 85 you get 3/4 of the original number
 |
|
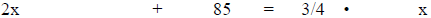
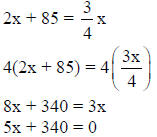| Clear the fraction . | |
| Solve for the unknown . | |
| 5x = -340 | Answer the question with a sentence. |
| x = -68 |
“The original number is -68.” See if -68 works in the problem. If you double -68 and then add 85, do you get 3/4 of -68? Yes, you do. Your answer must be correct. |
Example:
A 480 foot wire is cut into 3 pieces. The second piece is 3 times as long as the
first. The third piece is
4 times as long as the second. How long is each piece?
The question is, how long is each piece? Since there are 3 pieces, there are 3
“unknowns”.
We must let x = the length of one of the pieces. Which piece? Choose the one
that is the “most
unknown”. We know some things about the second and third pieces. We know nothing
about the first
piece, so we will
let x = the length of the first piece
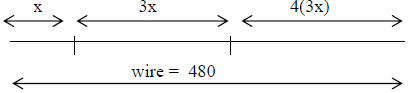
We can organize our information with a list or a picture.
| List Method | Picture Method |
|
x = the length of the first piece 3x = the length of the second piece 4(3x) = the length of the third piece 480 = total length of the wire |
 |
Now we need an equation. In this problem, common sense
gives us our equation. We know that the
sum of the lengths of the 3 pieces should equal the total length of the wire.
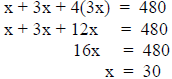
Answer with a sentence.
“The first piece is 30 feet long, the second is 90 feet long, and the third is
360 feet long.”
Check by seeing if your answer “works” in the original problem. Do you have 3
pieces? Yes. Is the
second piece 3 times as long as the first? Yes. Is the third piece 4 times as
long as the second? Yes.
Do the pieces add up to 480 feet of wire? Yes. Your answer works!
Example:
One angle of a triangle is 32 times as large as another. The measure of the
third angle is 10 degrees
greater than that of the smallest angle. How large are the angles?
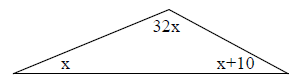
Let x = the measure of the smallest angle
| List Method | Picture Method |
|
x = the measure of the smallest angle 32x = the measure of the second angle x + 10 = the measure of the third angle |
 |
It is a fact from geometry that the three angles inside a
triangle will always sum to 180 degrees.
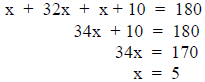
“The smallest angle is 5 degrees, the second is 160 degrees, and the third is 15
degrees.”
Example:
The sum of three consecutive odd integers is 189. What are the integers?
Let x = the first odd integer
|
“Consecutive” integers are 1 unit away from each other ( 1,2,3,4,...). “Consecutive odd” integers are 2 units away from each other ( 1,3,5,7,...) [“Consecutive even” integers are also 2 units away from each other ( 2,4,6,8,...)] |
The sum of the three odd integers is 189
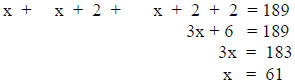
“The consecutive odd integers are 61, 63, and 65.”
Example:
The width of a rectangle is 3/4 of the length. The perimeter of the rectangle
becomes 50 cm when the
length and width are each increased by 2 cm. Find the length and the width.
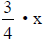| Let | x = the length of the rectangle |
 = the width of the rectangle |
If the length is increased by 2 cm it would be x + 2
If the width is increased by 2 cm it would be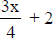 
When the length and width are increased by 2 cm, the perimeter of the rectangle
becomes 50 cm.
Perimeter equals 2 lengths + 2 widths (the distance all the way around the
rectangle).
2 · length + 2 · width = perimeter
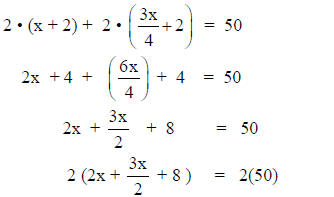Clear the fraction.
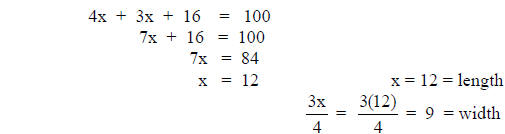
“The length of the rectangle is 12 cm and the width is 9
cm.”
Problems
1. Two less than 10 times a number is 118. What is the number?
2. The sum of 2 consecutive even integers is 106. What are the integers?
3. The perimeter of a rectangle is 1280. The width is 90 less than the length.
Find the width
and length.
4. The second angle of a triangle is three times as large as the first. The
third angle is
28 degrees less than the sum of the other 2 angles. What is the measure of each
angle?
Answers
1. 12
2. 52 and 54
3. Length is 365, width is 275
4. The angles are 26º, 78º, and 76º
| Prev | Next |