Add - Subtract POLYNOMIALS
A monomial is an algebraic expression that is a product of a real number and
one or more letters with
whole number exponents . A polynomial is an algebraic sum of monomials. Special
names are given
to polynomials of one, two and three terms ( monomial, binomial, trinomial ) and
all others are simply
called polynomial. The degree of a polynomial in one variable is the highest
power to which the
variable is raised. Polynomials of degree 2 are frequently called “ quadratic ”
and polynomials of
degree 3 are called “cubic”.
| The degree of a monomial in several variables is the sum of the
exponents of each variable . The degree of a polynomial in several variables is the highest degree of the monomials in the polynomial. |
Examples:
Monomials: 2, [degree 0], 3a, [degree 1],
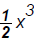 ,
[degree 3],
,
[degree 3],
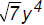 ,
[degree 4],
,
[degree 4],
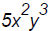 ,
[degree 5]
,
[degree 5]
Binomials :
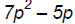 [degree 2],
[degree 2],
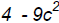 [degree 2], 3a – 6 [degree 1],
[degree 2], 3a – 6 [degree 1],
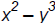 [degree 3]
[degree 3]
Trinomials:
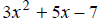 [degree 2],
[degree 2],
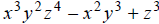 [degree 9]
[degree 9]
Addition of Polynomials : To add two or more polynomials use the basic
properties (associative,
commutative, distributive, etc.) and add the coefficients of like terms (or
combine like terms.)
|
Caution: Like terms must have the same letters
with the same exponents. Do not change exponents when |
Examples:
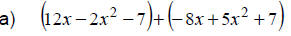 |
|
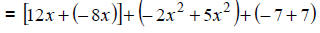 |
Apply the associative and commutative properties |
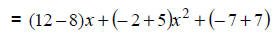 |
Apply the distributive property. |
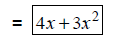 |
Add coefficients. |
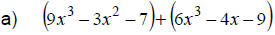 |
Watch signs and note that the middle terms aren ’t “similar”. |
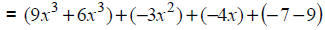 |
Apply the associative and commutative properties. |
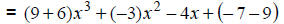 |
Apply the distributive property. |
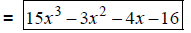 |
Add coefficients. |
Negation of a Polynomial: To negate a polynomial multiply each term by (-1).
Example:
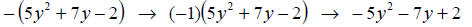
Subtraction of Polynomials : To subtract a polynomial from another you
must add the “opposite”
(or negate the polynomial following the “minus sign” and add the result
algebraically).
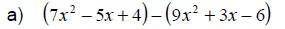 |
Watch the signs. |
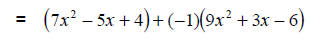 |
Change to (-1) times polynomial |
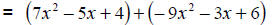 |
Distribute the (-1) over the 2nd polynomial. |
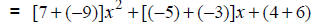 |
Apply the associative and commutative properties. |
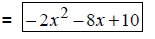 |
Add coefficients. |
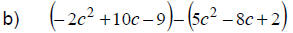 |
Watch the signs. |
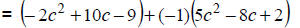 |
Change to (-1) times polynomial. |
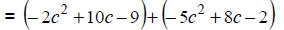 |
Distribute the (-1) over the 2nd polynomial. |
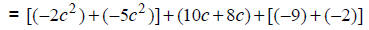 |
Apply associative and commutative properties. |
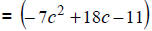 |
Add coefficients. |
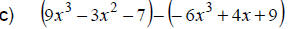 |
Note that the middle terms aren’t “similar”. |
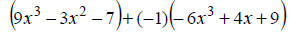 |
Watch the signs. Change to (-1) times polynomial. |
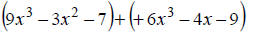 |
Distribute the (-1) over the 2nd polynomial. |
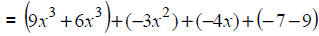 |
Apply the associative and commutative properties. |
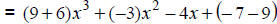 |
Apply the distributive property. |
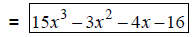 |
Add coefficients. |
| Prev | Next |