System of Linear Equations II

Algebrator can easily solve problems such as the one you posted on Yahoo Answers.

You start by entering it in an intuitive math editor. You may enter each equation on a line of its own and the software will solve this "system of two equations in two unknowns".

To control the method by which the system is solved, use the drop-down menu "Solution->Settings", where Elimination,

Substitution and Cramer rule are shown as options.

You can also let the software choose the best method by selecting "Best choice".

An example using your system of equations is described below.

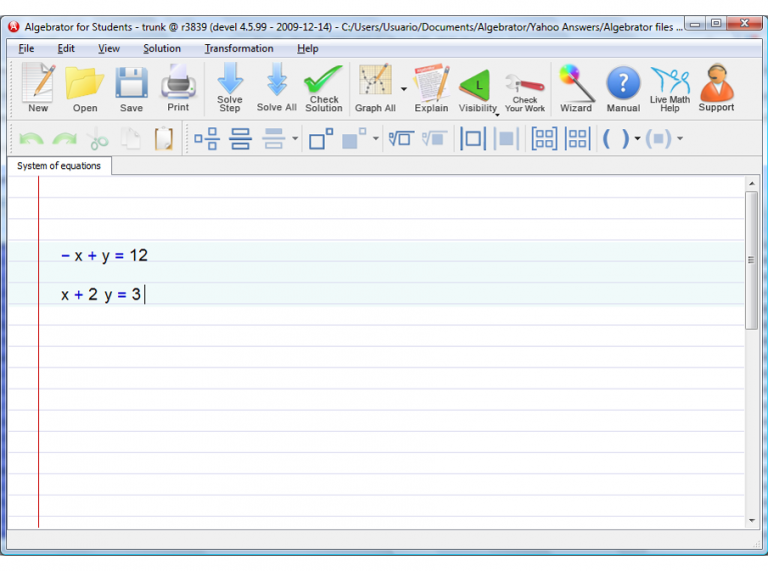
In this case I have selected "Best Choice" and Algebrator chose the "Elimination" method.

So the software starts by adding both equations.

Below, you can check the explanation given by Algebrator.

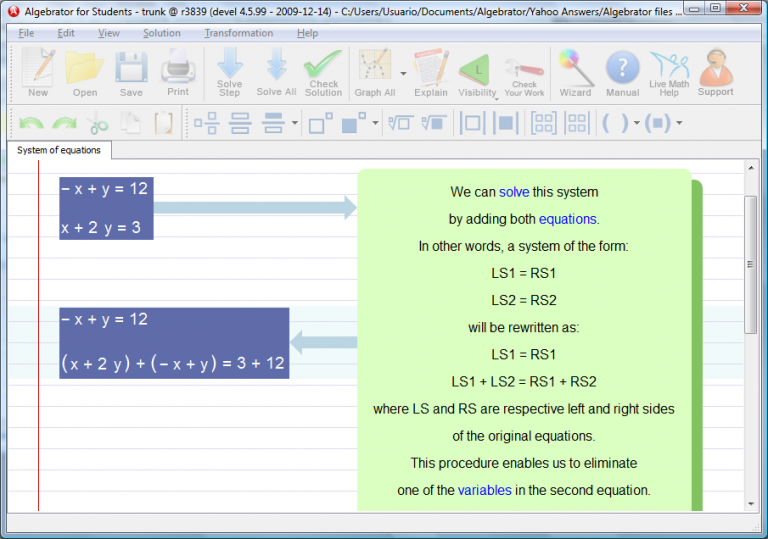
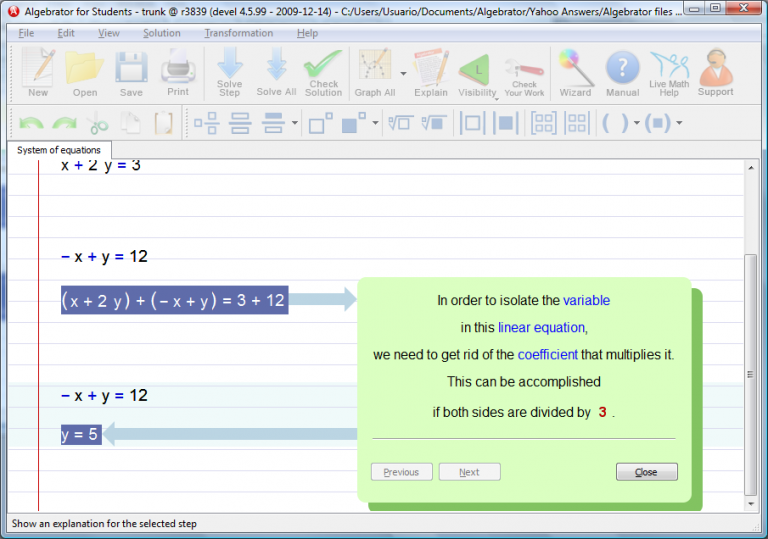
In order to isolate the variable, in this linear equation, we need to get rid of the coefficient that multiplies it.

This can be accomplished if both sides are divided by 3.

Explanation for this (or any other) step is just a click away.

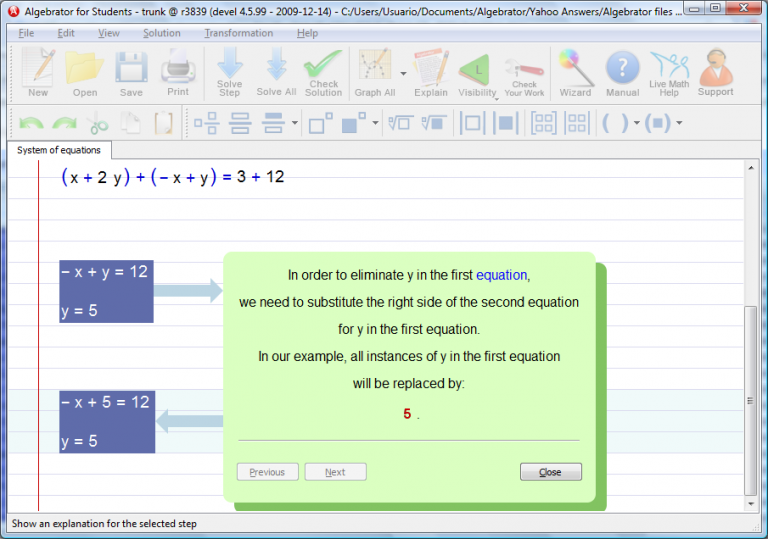
Some Important features are:

1.Flash demos, found under the drop-down menu "Help->Tutors".

The demos are also available online at "https://softmath.com/demos/", where you may simply select any of the ".htm"

files and the demo will play within your browser

2. Wizard button - for example, click the Wizard button and look under the category of "Line" to see the many useful

templates for exploring linear equations.

3. The Explain button, which provides the mathematical logic involved in the selected step.

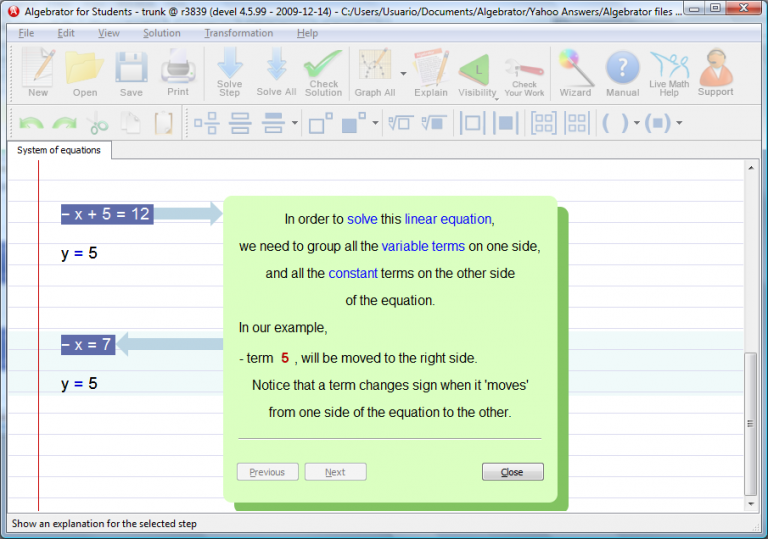
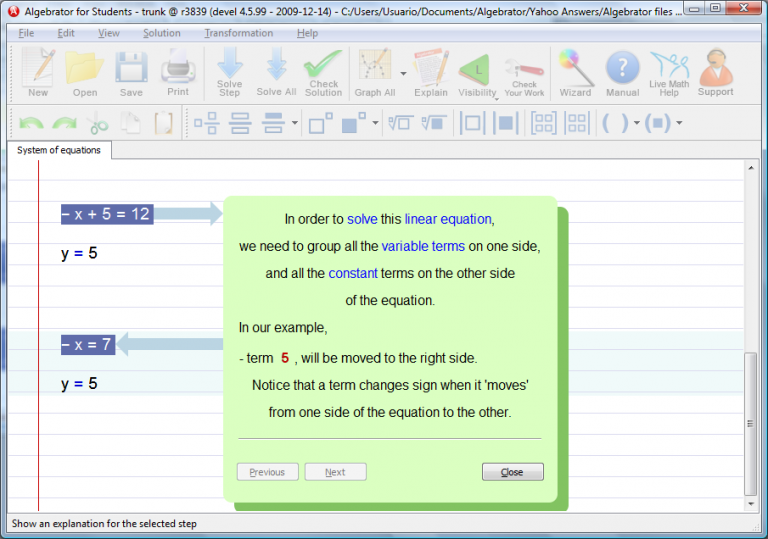
Solving this linear equation requires that we group all variable terms on one side and all constant terms on the other side.

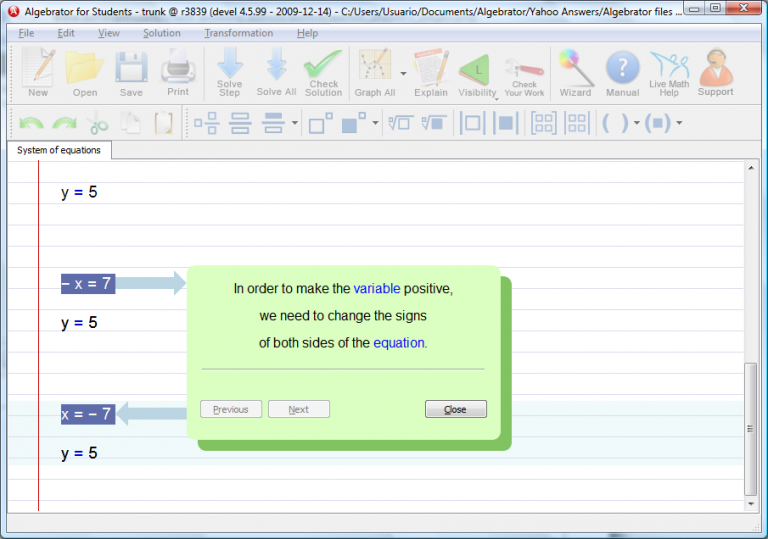
Entering any graphable equation directly into a new worksheet and pressing "Graph All" will first result in that equation being placed into its standard form prior to graphing. For linear equations the standard form is "y=mx+b", where "m" is the slope and "b" the y-intercept.

To solve the equation graphically, simply enter each equation on its own line within the same worksheet and then press "Graph All".

It is important to understand that anytime you are solving a system of equations you are answering the basic question "Do the graphs of these equation touch?". They may touch in one point (one solution), no points (no solutions) or an infinite number of points (i.e. the equations define the same line).

For this reason, it is always helpful to press "Graph All" even it you are not seeking a graphical solution, as this allows you to see a graph of the equations and better understand the numerical solution you obtained.