Parabola - Focus and Latus rectum: Graph, focus, direction, vertex, axis and directrix
Original question text:
Please help me in parabola problem.
This is my assignment:How to graph this parabola and what is the focus, direction, vertex, axis of parabola, directrix and latus rectum. Please help me. to understand this question.4y^2=-3x and -3x^2=15yThanks! ! !! ! ! !How can Algebrator help you with this problem?
Part V
Again, Algebrator can easily help you solve and understand your problem.
1) In order to find the latus rectum of a parabola you need to remember that the latus rectum is the chord that passes through the focus and is perpendicular to the axis.
So, in order to find the length of the latus rectum, we can do the following:
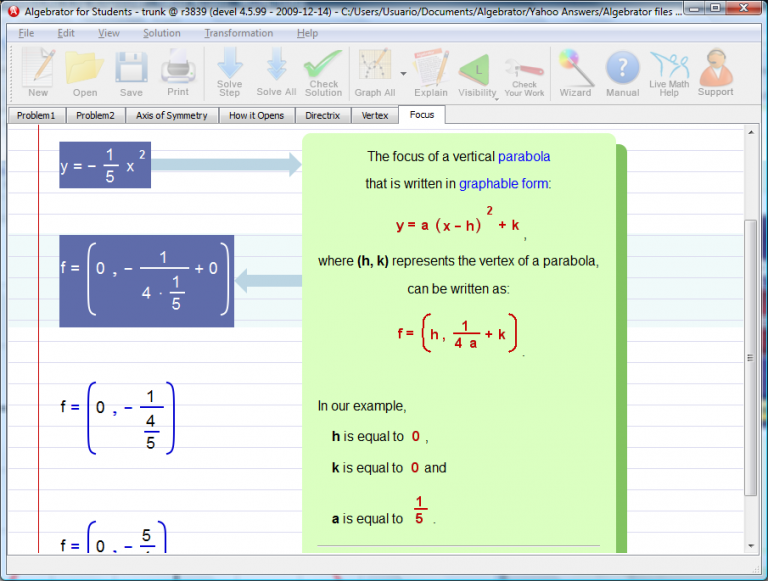
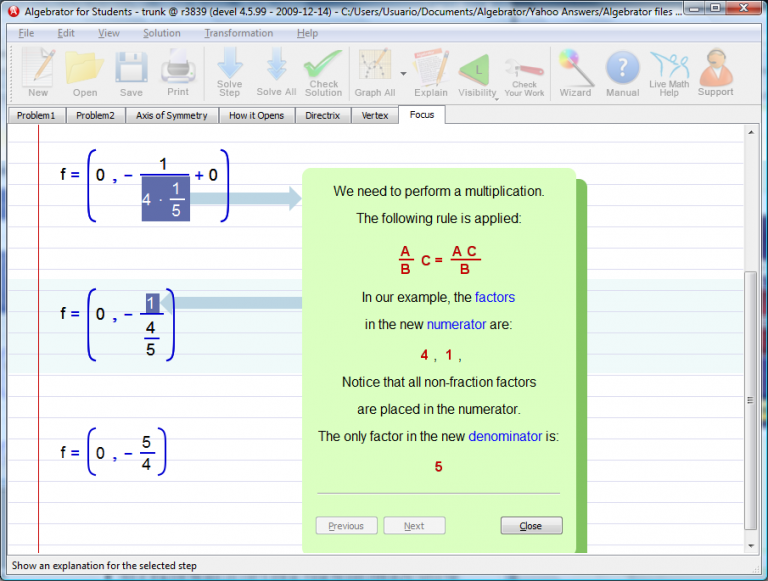
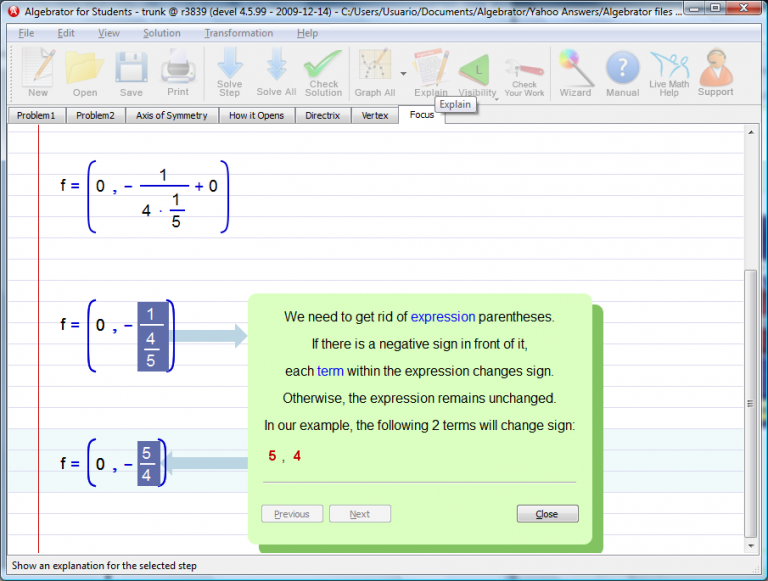
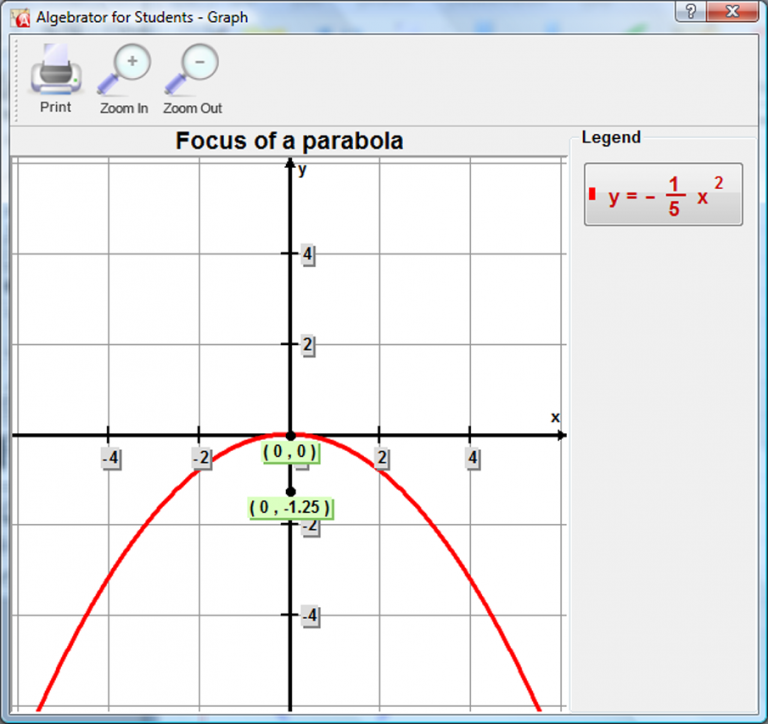
a) Find the focus of the parabola (by using the wizard "Focus of a parabola".
b) Find a point on the parabola that have the same y-coordinate as the focus (this is because the parabola is vertical). We accomplish this by finding the solutions of the given parabola for y = y-coordinate of the focus.
c) Find the distance between the points you have found by using the wizard "Distance between two points".
Now, We have to find points on the parabola that have the same y-coordinate as the focus (this is because the parabola is vertical).
We accomplish this by finding the solutions of the given parabola for y = y-coordinate of the focus (which in our example is -5/4.
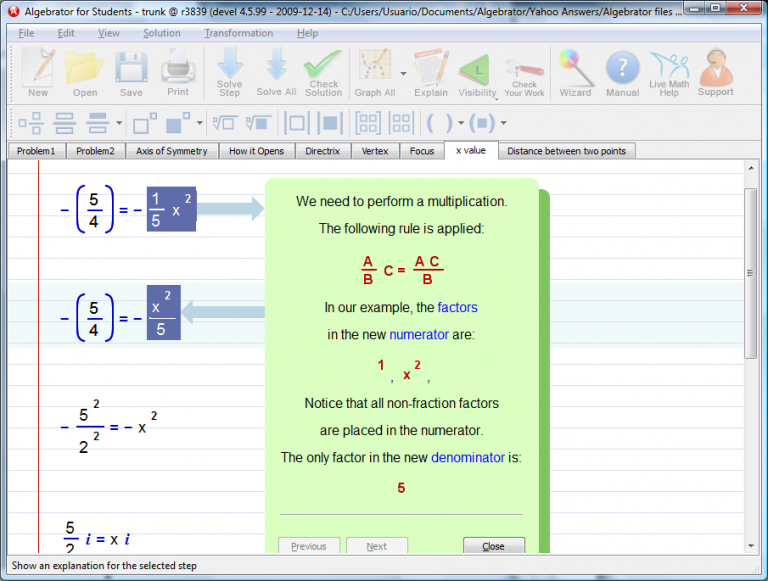
We can see the rest of the solution process by pressing the "solve" button several times.
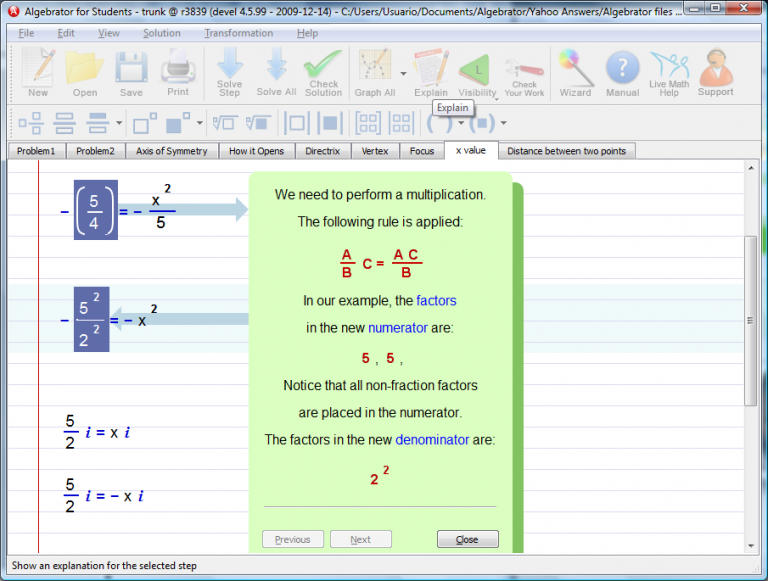
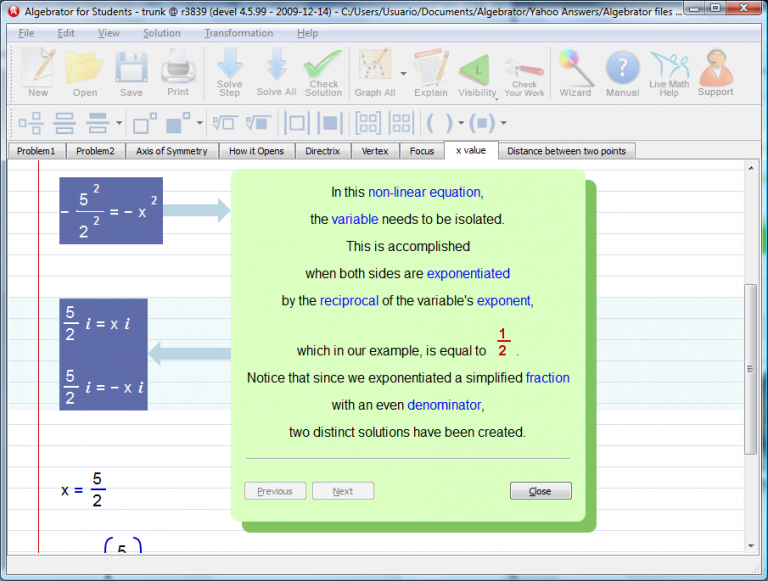
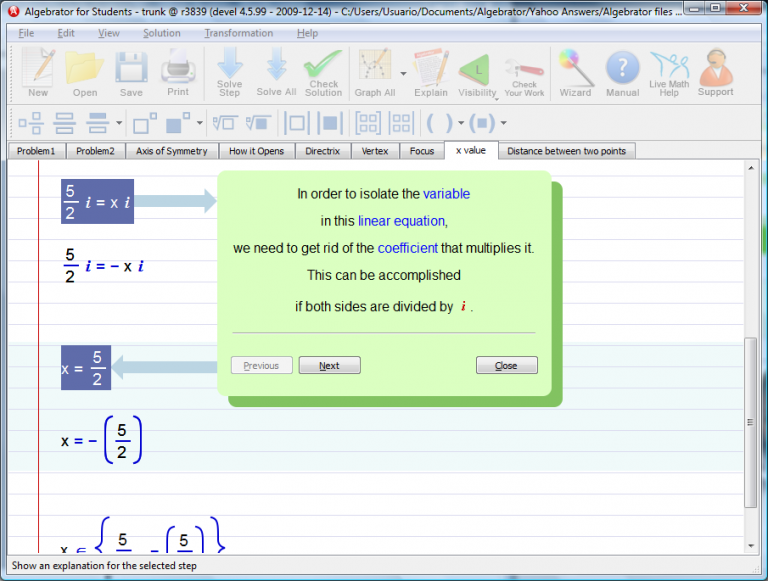
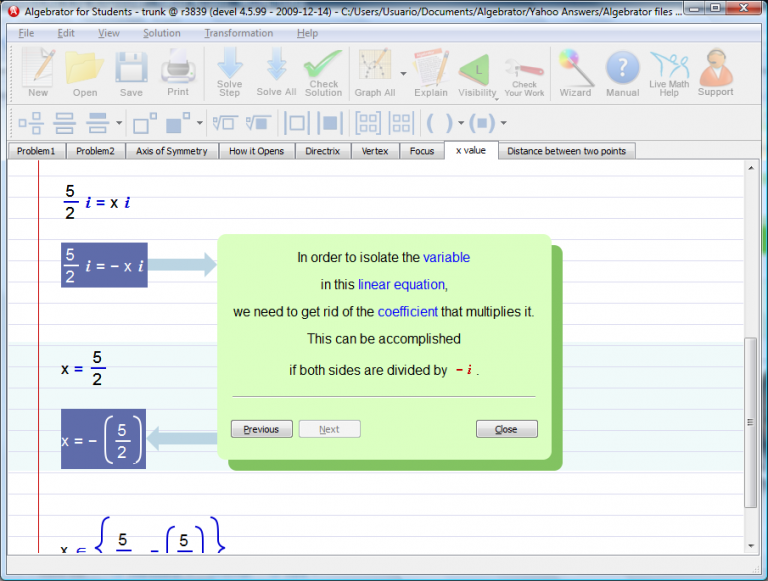
Finally we arrive to the solution set of points that have the same y-coordinate as the focus.
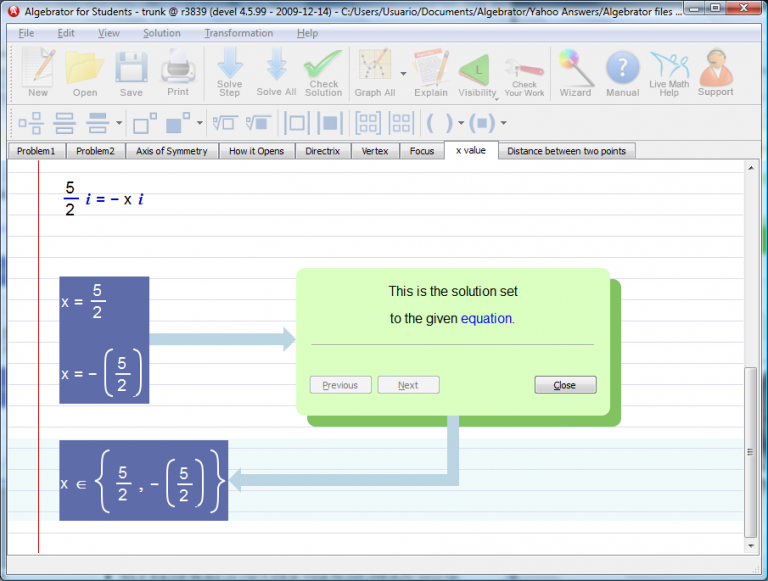
So now the last step.
We have to input the coordinates for both sets of points in our "Distance between two points" Line Wizard.
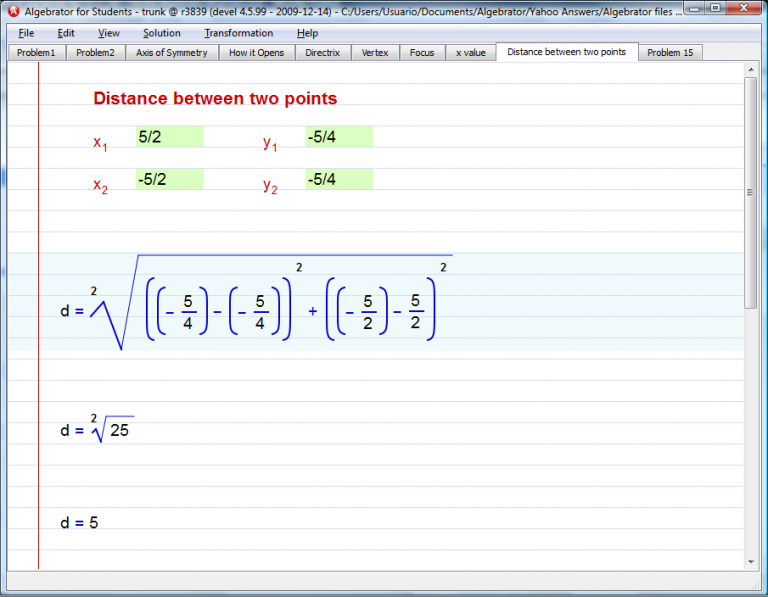
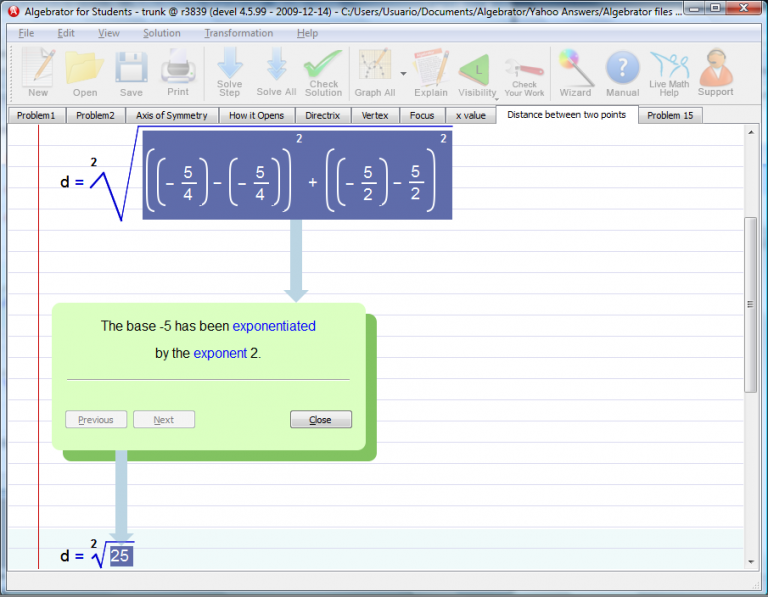
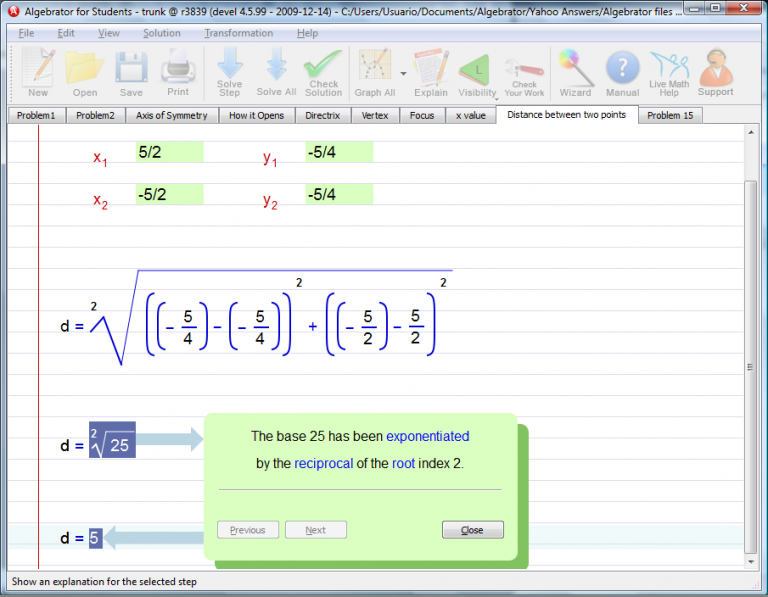
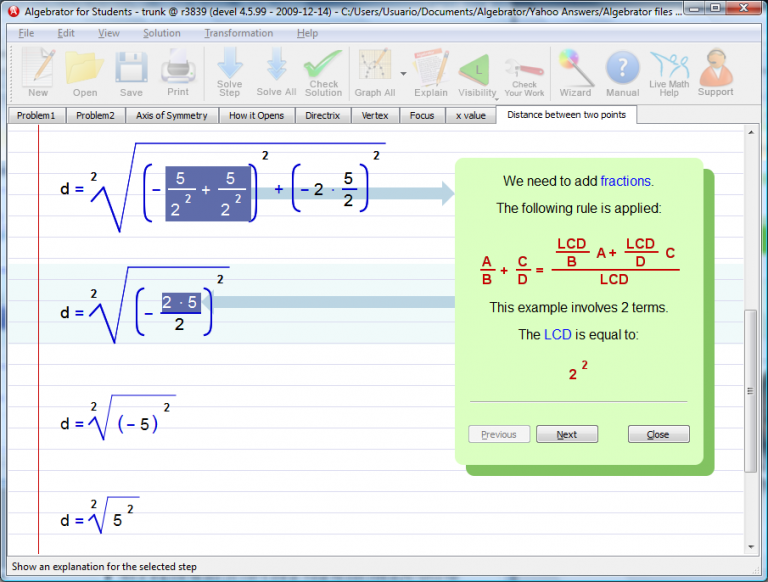
Finally you will see the latus rectum graphed.
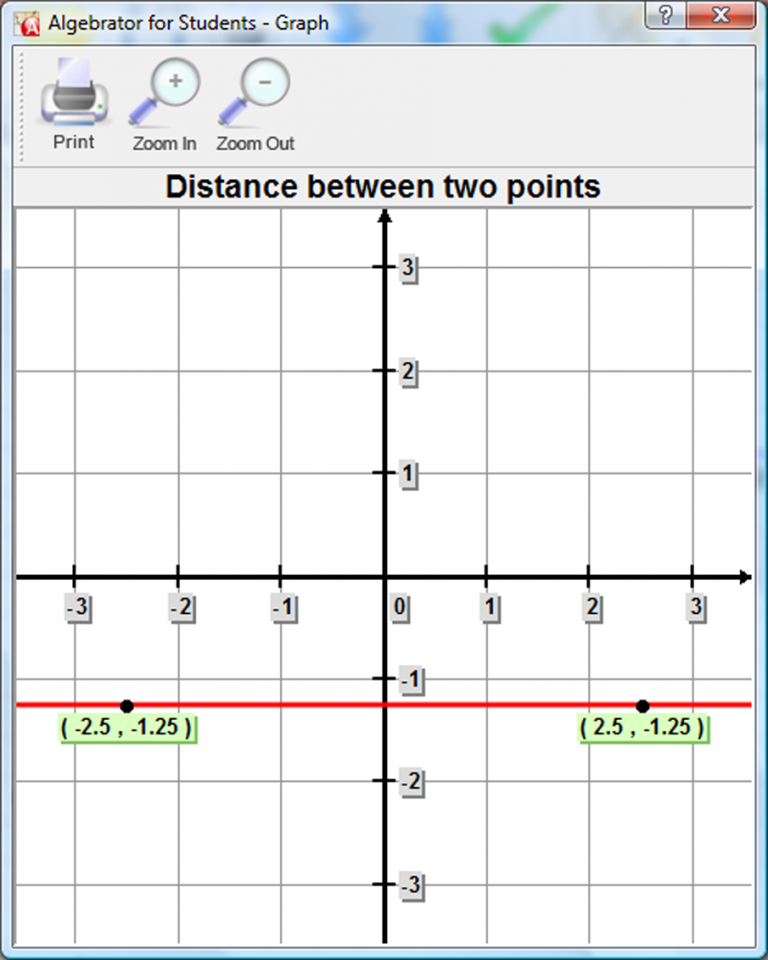
| Prev | See Full List of Math Problems Explained in Detail | Next |

