Algebra Review

1 Groups

Definition 1.1 A semigroup (G, ·) is a set G with a binary operation · such that:

Axiom 1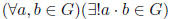

Axiom 2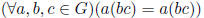

Definition 1.2 A group (G, ·) is a semigroup such that:

Axiom 3 (Identity element)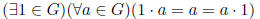

Axiom 4 (Inverse)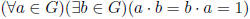

Multiplicative Notation :

• ab = a · b

• In Axiom 4, b = a^-1

Additive Notation :

• Binary operation ‘+’

• Identity becomes ‘0’

• Additive inverse ‘-a’

The size of G as a set, which is denoted |G|, is called the order of G.

Definition 1.3 G is an abelian group if G is a group such that .

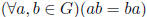Definition 1.4 H 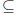G is a subgroup of G (denoted H ≤ G) if

1. 1 ∈ H

2. H is closed under the binary operation

3. H is closed under inverses

Definition 1.5 Let H ≤ G. The sets of the form a ·H := {ah : h ∈ H} for a ∈G are the left
cosets of G. The left cosets partition G. Right cosets are defined analogously.

Definition 1.6 |G : H| = number of left cosets of H in G is called the index of H in G.

Exercise 1.7 Prove that the number of left cosets is the same as the number of right cosets,
even if G is infinite. (Hint: construct a bijection between the left and the right cosets.)

Exercise 1.8 Prove: if G is finite then the left and the right cosests have a common system
of represetatives, i. e., there exists a set T of size |T| = |G : H| such that T contains exactly
one element from every left coset as well as from every right coset.

Exercise 1.9 (Lagrange) If H ≤ G then |G| = |H| · |G : H|. Therefore, if |G| < ∞ then


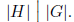
Exercise 1.10 Prove: the intersection of subgroups is a subgroup.

Definition 1.11 Let S 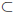G. We define the subgroup of G generated by S by



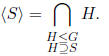
A group is cyclic if it is generated by an element (|S| = 1).

Exercise 1.12 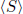is the set of all products of elements of S and inverses of elements of S.

Example 1.13 Let S = {a, b}. Then .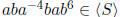

Example 1.14 If |S| = 1 and S = {g} then .

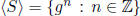Exercise 1.15 If G is cylic then

1. if |G| = 1 then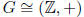

2. if |G| = n then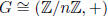

Definition 1.16 The order of an element g ∈ G is the order of the cyclic group generated
by .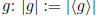

Exercise 1.17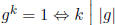

Exercise 1.18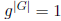

Exercise 1.19 (Euler - Fermat)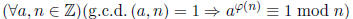

Exercise 1.20 If G is an abelian group then

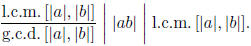
This shows that if g.c.d. [|a|, |b|] = 1 then |ab| = l.c.m. [|a|, |b|].

Definition 1.21 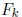is a free group of rank k on free generators 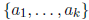if the
products of the 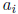and the 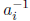give 1 only by explicit cancellation.

Example 1.22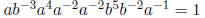

Exercise+ 1.23 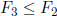. In fact, .

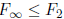Definition 1.24 For a commutative ring R, the special linear group SL(n,R) is the group
of those n × n matrices 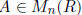with det(A) = 1. (More about rings below; we assume all
rings have an identity element.)

Exercise* 1.25 (Sanov) 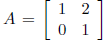and A^T (A transpose) freely generate a free group
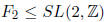. (Hint: for , let 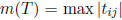. Show that 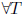there is
at most one 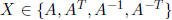such that m(T) ≥ m(TX).)

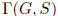Definition 1.26 Let G be a group and S G \ 1. The Cayley graph has G for its
vertex set ; elements g, h ∈ G are adjacent if 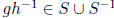(where ).

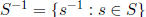Exercise 1.27 Prove: 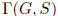is connected if and only if S generates G.

Exercise 1.28 Suppose G = . Then 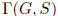is bipartite if and only if G has a subgroup
N of index 2 such that ;.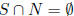

Exercise 1.29 Let S be a minimal set of generators of G, i. e., no proper subset of S generates
G. Prove: .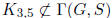

A theorem of 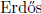and Hajnal states that if an (infinite) graph X does not contain 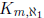as
a subgraph (for some m ∈N) then 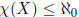. As a consequence of the preceding exercise , if
S is a minimal set of generators then .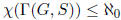

Exercise 1.30 Prove that every group G has a set S of generators such that .
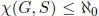Hint. Not every group has a minimal set of generators (e. g., (Q, +) does not). But every
group has a sequentially non-redundant set of generators, 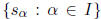, where I is a well-ordered
set and 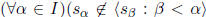. Prove that if S is sequentially non-redundant
then .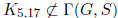

Exercise 1.31 If a regular graph of degree r with n vertices has girth g then

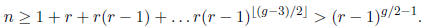
Consequently, .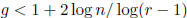

On the other hand, and Sachs proved for every r ≥ 3 there exist r-regular graphs of girth
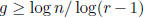. The following problem addresses the question of explicit construction
of a 4-regular graph with large girth. The girth will be optimal within a constant factor .

Exercise 1.32 (Margulis) Let G = SL(2, p) := SL(2,Z/pZ). Let S = {A,B} where
and B = A^T (A transpose). Note that |G| < p³ and has degree 4. Prove
that the girth of is 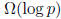 . (Hint. Use Sanov's Theorem and the submultiplicativity
of matrix norm.

2 Rings

Definition 2.1 A ring (R,+, ·) is an abelian group (R, +) and semigroup (R, ·) such that:

• ( Distributivity ) 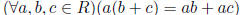and ((b + c)a = ba + ca)

Exercise 2.2 In a ring R,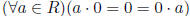

Definition 2.3 (R,+, ·) is a commutative if (R, ·) is abelian.

Definition 2.4 R is a ring with identity if (R, ·) satisfies Axiom 3 (semigroup with identity)
and 1 ≠ 0.

CONVENTION. By “rings” we shall always mean rings with identity.

Definition 2.5 a ∈ R is a unit if .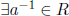

Exercise 2.6 The units of R form a multiplicative group denoted .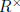

Example 2.7 Let R be a ring.

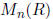• := set of n × n matrices over R is a ring

Exercise 2.8 Let R be a commutative ring. GL(n,R) denotes the group of units of .

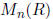Prove: 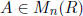belongs to GL(R) if and only if .

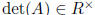Example 2.9 mod m residue classes form a ring, denoted Z/mZ.

Exercise 2.10 What is the order of the group of units of Z/mZ?

Definition 2.11 a ∈ R is a left zero divisor if a ≠ 0 and 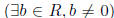(ab = 0). Right
zero divisors are defined analogously.

Definition 2.12 a ∈R is a zero-divisor if a is a left OR a right zero-divisor.

Exercise 2.13

1. If 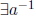then a is not a zero-divisor.

2. The coverse is false.

3. The converse is true if R is finite.

4. The converse is true if 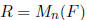where F is a field. In this case, A ∈ R is a zero-divisor
if and only if det(A) = 0.

Definition 2.14 An integral domain is a commutative ring with no zero-divisors.

Definition 2.15 A division ring is a ring where all nonzero elements are units, i. e.,
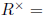
R \ {0}.