A Math Primer
Slope
The slope of a line is a measure of how “tilted” the
line is . A highway sign might say something like
“6% grade ahead.” What does this mean, other than
that you hope your brakes work? What it means is
that the ratio of your drop in altitude to your
horizontal distance is 6%, or 6/100. In other words, if
you move 100 feet forward, you will drop 6 feet; if
you move 200 feet forward, you will drop 12 feet,
and so on.

We measure the slope of lines in much the same way,
although we do not convert the result to a percent.
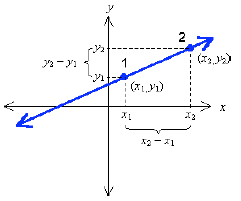
Suppose we have a graph of an unknown straight
line. Pick any two different points on the line and
label them point 1 and point 2:
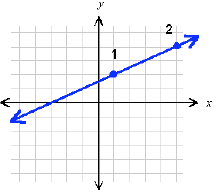
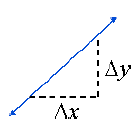
In moving from point 1 to point 2, we cover 4 steps
horizontally (the x direction) and 2 steps vertically
(the y direction):
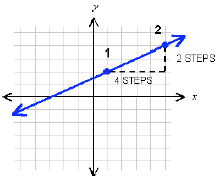
Therefore, the ratio of the change in altitude to the
change in horizontal distance is 2 to 4. Expressing it
as a fraction and reducing , we say that the slope of
this line is
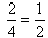
To formalize this procedure a bit, we need to think
about the two points in terms of their x and y
coordinates.
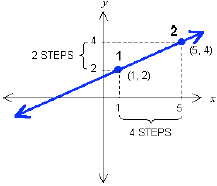
Now you should be able to see that the horizontal
displacement is the difference between the x
coordinates of the two points, or
4 = 5 – 1,
and the vertical displacement is the difference
between the y coordinates, or
2 = 4 – 2.
In general, if we say that the coordinates of point 1
are 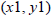 and the coordinates of point 2 are
and the coordinates of point 2 are
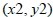 ,
,
then we can define the slope m as follows:
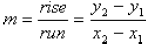
where 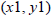 and
and
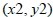 are any two distinct
are any two distinct
points on the line.
![]() It is customary (in
the US) to use the letter m to
It is customary (in
the US) to use the letter m to
represent slope. No one knows why.
![]() It makes no difference which two points are used
It makes no difference which two points are used
for point 1 and point 2. If they were switched,
both the numerator and the denominator of the
fraction would be changed to the opposite sign,
giving exactly the same result.
![]() Many people find it useful to remember this
Many people find it useful to remember this
formula as “slope is rise over run.”
![]() Another common notation is m = Δy/Δx, where
Another common notation is m = Δy/Δx, where
the Greek letter delta (Δ) means “the change in.”
The slope is a ratio of how much y changes per
change in x:
Horizontal Lines
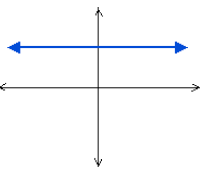
A horizontal line has zero slope, because there is no
change in y as x increases. Thus, any two points will
have the same y coordinates, and since 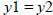 ,
,
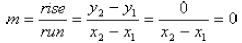
Vertical Lines
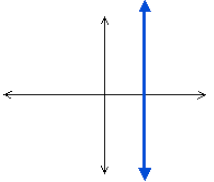
A vertical line presents a different problem. If you
look at the formula
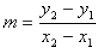
you see that there is a problem with the denominator.
It is not possible to get two different values for
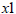 and
and
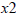 , because if x changes then you are not on the
, because if x changes then you are not on the
vertical line anymore. Any two points on a vertical
line will have the same x coordinates, and so
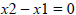 . Since the denominator of a fraction
. Since the denominator of a fraction
cannot be zero, we have to say that a vertical line
has undefined slope. Do not confuse this with the
case of the horizontal line, which has a well-defined
slope that just happens to equal zero.
Positive and Negative Slope
The x coordinate increases to the right, so moving
from left to right is motion in the positive x direction.
Suppose that you are going uphill as you move in the
positive x direction. Then both your x and y
coordinates are increasing, so the ratio of rise over
run will be positive—you will have a positive
increase in y for a positive increase in x. On the other
hand, if you are going downhill as you move from
left to right, then the ratio of rise over run will be
negative because you lose height for a given positive
increase in x. The thing to remember is:
As you go from left to right,
![]() Uphill = Positive Slope
Uphill = Positive Slope
![]() Downhill = Negative
Slope
Downhill = Negative
Slope
And of course, no change in height means that the
line has zero slope.
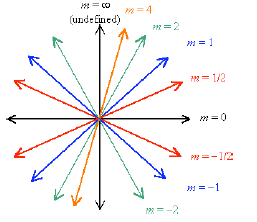
Some Slopes
Intercepts
Two lines can have the same slope and be in
different places on the graph. This means that in
addition to describing the slope of a line we need
some way to specify exactly where the line is on the
graph. This can be accomplished by specifying one
particular point that the line passes through.
Although any point will do, it is conventional to
specify the point where the line crosses the y-axis.
This point is called the y-intercept, and is usually
denoted by the letter b. Note that every line except
vertical lines will cross the y-axis at some point, and
we have to handle vertical lines as a special case
anyway because we cannot define a slope for them.
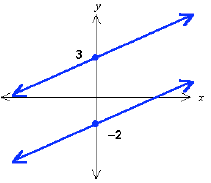
Same Slopes, Different y-Intercepts
Equations
The equation of a line gives the mathematical
relationship between the x and y coordinates of any
point on the line.
Let’s return to the example we used in graphing
functions. The equation
y = 2x – 1
produces the following graph:

This line evidently has a slope of 2 and a y intercept
equal to –1. The numbers 2 and –1 also appear in the
equation—the coefficient of x is 2, and the additive
constant is –1. This is not a coincidence, but is due to
the standard form in which the equation was written.
Standard Form (Slope- Intercept Form )
If a linear equation in two unknowns is written in the
form
y = mx + b
where m and b are any two real numbers , then the
graph will be a straight line with a slope of m and a y
intercept equal to b.
Point-Slope Form
As mentioned earlier, a line is fully described by
giving its slope and one distinct point that the line
passes through. While this point is customarily the y
intercept, it does not need to be. If you want to
describe a line with a given slope m that passes
through a given point ![]() , the formula is
, the formula is
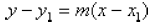
To help remember this formula, think of solving it
for m:
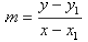
Since the point (x, y) is an arbitrary point on the line
and the point ![]() is another point on the line, this
is another point on the line, this
is nothing more than the definition of slope for that
line.
Two-Point Form
Another way to completely specify a line is to give
two different points that the line passes through. If
you are given that the line passes through the points
![]() and
and
![]() , the formula is
, the formula is
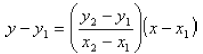
This formula is also easy to remember if you notice
that it is just the same as the point-slope form with
the slope m replaced by the definition of slope,
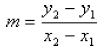
| Prev | Next |