Math 101 Review Sheet for Exam #2

5 Exponents and Polynomials

5.1 Integer Exponents

All of the rules you could possibly ever need to know are summarized
on pages 289-290 in the big purple box. You will be asked to apply
these rules.

Problems 1-88 are practice problems leading up to the problems
that we need to be able to solve. If you feel confident, dive into
any of 107-124. Do enough problems so you can solve 121 and 123
confidently , this looks like a good order of difficulty to me.

In addition, you might want to try the following. Simplify until
all exponents are positive,

1.

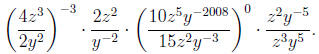
Don’t worry about looking at scientific notation. This wasn’t
covered in the homework or in class.

5.2 Adding and Subtracting Polynomials

This section is really practice leading up to the important stuff:
multiplying and dividing polynomials . One common item you need
to be quick with is subtracting polynomials, because this shows up
so often when doing polynomial long division. You may want to try
problems 57, 58, 59, 60 or just wait until the long division section
to get practice doing this.

5.3
Skip this section.

5.4 Multiplying Polynomials

It’s important you know how to do simple multiplication, such as
8-13 any.

It’s also important you know how to multiply polynomials where
the FOIL method doesn’t work. (The big problem with this method
is it doesn’t generalize). 15-23 all look like excellent problems to take
a peek at.

83 and 84 also look like excellent problems.

5.5 What’s next? Polynomial Division

What can I say. Know how to do polynomial long division. Know
how to deal with the remainder if it’ s not zero .

I think the most common error will be not subtracting all terms
when it comes time to do the subtraction.

Problems 17-46 all look like excellent problems.

6 The Backwards Problem, Factoring Polynomials

After learning how to add, subtract, multiply and divide polynomials,
now we do it in reverse order. Sections 6-1 through 6-4 seem a
bit jumbled up. I’ll point out what’s important from these sections,
then give you a lot of practice problems.

6.1 Greatest Common Factors; Factoring by Grouping

6.2 Factoring Trinomials

This section is really the heart of the chapter. The goal is to get to
the point where you can factor trinomials which are polynomials of
the form ax² + bx + c.

For our purposes, we will not ask you to determine if a polynomial
is prime. Whatever problem shows up on the exam, you will be able
to factor it.

6.3 Special Factoring

We don’t want you to have to memorize a lot of formulas . One
important factoring to keep in mind is using the formula

x² − y² = (x + y)(x − y).

For example, this can be used to factor

x² − 169.

6.4 A General Approach to Factoring

This really seems like a better review section than section inside the
chapter. Rather than work on these problems (there are many who
are prime, and some of them ask you to use special factorings that
we didn’t cover), I’ll give you practice problems here.

One thing to keep in mind is every time you’re asked to factor
a polynomial, first look for a common factor that can be pulled
out. This will make your life so much easier! Remember this when
working on these problems.

2. Factor:

a) x² + 4x − 21.

b) y² + 3y − 10.

c) a² + 3a − 130.

d) 4x² + 32x + 28.

e) x³ − 4x.

f) j² − j − 56.

g) 3x² + 3x − 6.

h) z³ − 2z² − 35z.

i) 2x² − 18.

j) y² + 3y − 130.

k) z³ − 4z²

l) 5k² − 20k + 225.

m) p² − 24p + 144.

n) n² + 14n + 49.

6.5 Solving Equations by Factoring

Do the homework problems. Below is an extremely brief description
of what’s in this section.

This is where we solve our first non- linear equation ! In order to
make any headway, we need to zero factor property , defined on page
360.

There are two tools to keep in mind when solving these problems.
First, the problem may be handed to you on a silver platter, like
solve

3.
(x − 5)(x + 60) = 0.

More likely, the problem will require a bit of work, namely factoring
a trinomial, and before that can be done you need to get all
your terms to one side . Similar to solve

4.
2x² = 3 − x.

Sometimes when trying to solve something like

(3y + 2)(y − 3) = 7y − 1

one needs to do a bit of work. Now with this problem, some idiot
decided to to a half job of factoring it. The left hand side is factored,
but in this case it doesn’t do us any good!

The tool to keep in mind, with a problem like this, is to multiply
everything out first. Then after doing that, you can get all terms to
one side, and you’ve reduced it down to factoring a trinomial.

So, with that being said,
5. Find the solution set for

(3y + 2)(y − 3) = 7y − 1.