Zeros of Polynomials
25. Start with p(x) = −6x3 + 4x2 + 16x. Factor out the
gcf (−2x in this case), then
use the ac- method to complete the factorization.
p(x) = −2x[3x2 − 2x − 8]
p(x) = −2x[3x2 − 6x + 4x − 8]
p(x) = −2x[3x(x − 2) + 4(x − 2)]
p(x) = −2x(3x + 4)(x − 2)
Set
0 = −2x(3x + 4)(x − 2)
and use the zero product property to write
−2x = 0 or 3x + 4 = 0 or x − 2 = 0.
Solving , the zeros are x = 0, −4/3, and 2.
27. Start with p(x) = −2x7 − 10x6 + 8x5 + 40x4. Factor
out the gcf (−2x4 in this
case), then use grouping and difference of squares to complete the
factorization.
p(x) = −2x4[x3 + 5x2 − 4x − 20]
p(x) = −2x4[x2(x + 5) − 4(x + 5)]
p(x) = −2x4(x2 − 4)(x + 5)
p(x) = −2x4(x + 2)(x − 2)(x + 5)
Set
0 = −2x4(x + 2)(x − 2)(x + 5)
and use the zero product property to write
−2x4 = 0 or x + 2 = 0 or x − 2 = 0 or x + 5 = 0.
Solving, the zeros are x = 0, −2, 2, and −5.
29. The graph of the polynomial
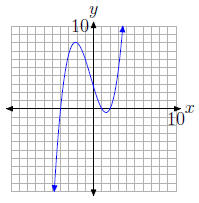
intercepts the x -axis at (−4, 0), (1, 0), and (2, 0). Hence, the zeros of the
polynomial
are −4, 1, and 2.
31. The graph of the polynomial
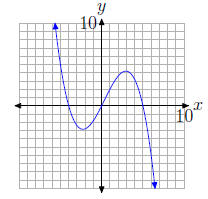
intercepts the x-axis at (−4, 0), (0, 0), and (5, 0). Hence, the zeros of the
polynomial
are −4, 0, and 5.
33. The graph of the polynomial
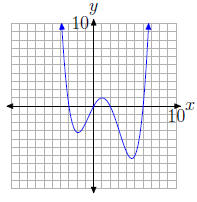
intercepts the x-axis at (−3, 0), (0, 0), (2, 0), and (6, 0). Hence, the zeros
of the polynomial
are −3, 0, 2, and 6.
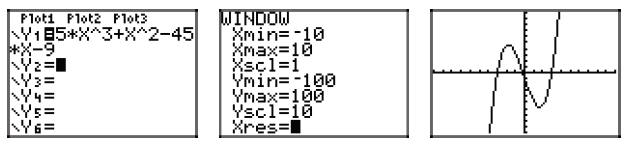
35. Factor p (x) = 5x3 + x2 − 45x − 9 by grouping, then
complete the factorization
with the difference of squares pattern .
p(x) = x2(5x + 1) − 9(5x + 1)
p(x) = (x2 − 9)(5x + 1)
p(x) = (x + 3)(x − 3)(5x + 1)
Using the zero product property , the zeros are −3, 3, and
−1/5. Hence, the graph
of the polynomial must intercept the x-axis at (−3, 0), (3, 0), and (−1/5, 0).
Further,
the leading term of the polynomial is 5x3, so the polynomial must have the same end-behavior
as y = 5x3, namely, it must rise from negative infinity, wiggle through its
x-intercepts, then rise to positive infinity . The sketch with the appropriate
zeros and
end behavior follows.
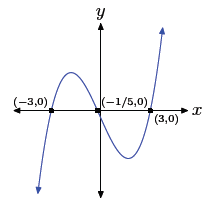
Checking on the calculator .
37. Factor p(x) = 4x3 − 12x2 − 9x + 27 by grouping, then complete the
factorization
with the difference of squares pattern.
p(x) = 4x2(x − 3) − 9(x − 3)
p(x) = (4x2 − 9)(x − 3)
p(x) = (2x + 3)(2x − 3)(x − 3)
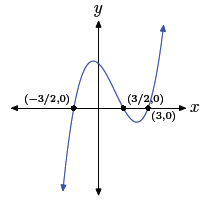
Using the zero product property, the zeros are −3/2, 3/2,
and 3. Hence, the graph
of the polynomial must intercept the x-axis at (−3/2, 0), (3/2, 0), and (3, 0).
Further,
the leading term of the polynomial is 4x3, so the polynomial must have the same
end-behavior
as y = 4x3, namely, it must rise from negative infinity, wiggle through its
x-intercepts, then rise to positive infinity. The sketch with the appropriate
zeros and
end behavior follows.
Checking on the calculator.
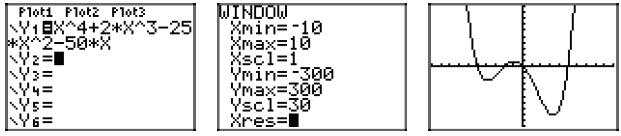
39. Start with p(x) = x4 + 2x3 − 25x2 − 50x, then factor out the gcf (x in
this case).
Then, factor by grouping and complete the factorization with the difference of
squares
pattern.
p(x) = x[x3 + 2x2 − 25x − 50]
p(x) = x[x2(x + 2) − 25(x + 2)]
p(x) = x(x2 − 25)(x + 2)
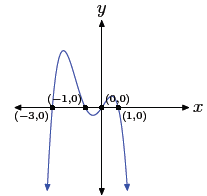
p(x) = x(x + 5)(x − 5)(x + 2)
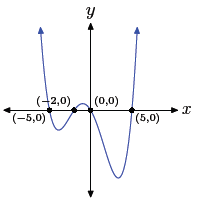
Using the zero product property, the zeros are 0, −5, 5,
and −2. Hence, the graph of
the polynomial must intercept the x-axis at (0, 0), (−5, 0), (5, 0), and (−2,
0). Further,
the leading term of the polynomial is x4, so the polynomial must have the same
end-behavior
as y = x4, namely, it must fall from positive infinity, wiggle through its
x-intercepts, then rise to positive infinity. The sketch with the appropriate
zeros and
end behavior follows.
Checking on the calculator.
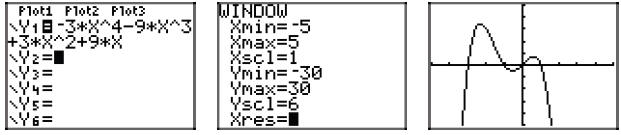
41. Start with p(x) = −3x4 − 9x3 + 3x2 + 9x, then factor out the gcf (−3x in
this
case). Then, factor by grouping and complete the factorization with the
difference of
squares pattern.
p(x) = −3x[x3 + 3x2 − x − 3]
p(x) = −3x[x2(x + 3) − 1(x + 3)]
p(x) = −3x(x2 − 1)(x + 3)
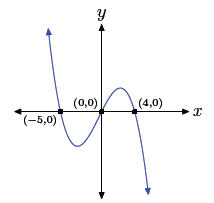
p(x) = −3x(x + 1)(x − 1)(x + 3)
Using the zero product property, the zeros are 0, −1, 1,
and −3. Hence, the graph of
the polynomial must intercept the x-axis at (0, 0), (−1, 0), (1, 0), and (−3,
0). Further,
the leading term of the polynomial is −3x4, so the polynomial must have the same
end-behavior as y = −3x4, namely, it must rise from negative infinity, wiggle
through
its x-intercepts, then fall back to negative infinity . The sketch with the
appropriate
zeros and end behavior follows.
Checking on the calculator.
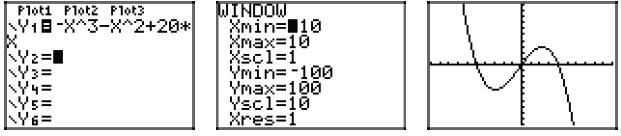
43. Start with p(x) = −x3−x2+20x, then factor out the gcf (−x in this case).
Then,
complete the factorization with the ac- method .
p(x) = −x[x2 + x − 20]
p(x) = −x(x + 5)(x − 4)
Using the zero product property, the zeros are 0, −5, and
4. Hence, the graph of the
polynomial must intercept the x-axis at (0, 0), (−5, 0), and (4, 0). Further,
the leading
term of the polynomial is −x3, so the polynomial must have the same
end-behavior as
y = −x3, namely, it must fall from positive infinity, wiggle through its
x-intercepts,
then fall to negative infinity. The sketch with the appropriate zeros and end
behavior
follows.
Checking on the calculator.
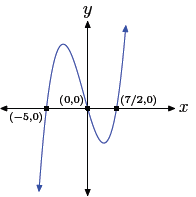
45. Start with p(x) = 2x3 +3x2 −35x, then factor out the gcf (x in this case).
Then,
complete the factorization with the ac-method.
p(x) = x[2x2 + 3x − 35]
p(x) = x[2x2 − 7x + 10x − 35]
p(x) = x[x(2x − 7) + 5(2x − 7)]
p(x) = x(x + 5)(2x − 7)
Using the zero product property, the zeros are 0, −5, and
7/2. Hence, the graph of
the polynomial must intercept the x-axis at (0, 0), (−5, 0), and (7/2, 0).
Further, the
leading term of the polynomial is 2x3, so the polynomial must have the same
end-behavior
as y = 2x3, namely, it must rise from negative infinity, wiggle through its
x-intercepts, then rise to positive infinity. The sketch with the appropriate
zeros and
end behavior follows.
Checking on the calculator.
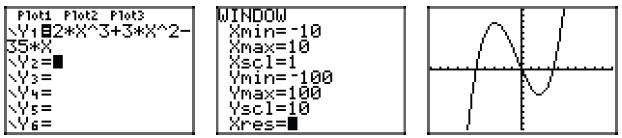
| Prev | Next |