rational exponents
Math D : 7.2
We de ne rational exponents to have the same properties as
integer expo-
nents. Suppose
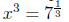
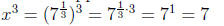
so x3 = 7 so x is the number whose cube is 7 so
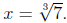
But we started with
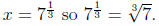
De nition 0.1 If
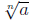 represents a real number and n 2 is an integer,
represents a real number and n 2 is an integer,
then
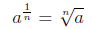
If a is negative , n must be odd.
Example 0.1 Converting from
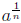
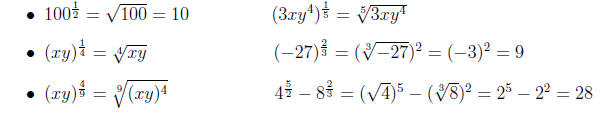
De nition 0.2 If
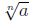 represents a real number , m/n is a positive rational
represents a real number , m/n is a positive rational
number reduced to lowest terms, and n ≥ 2 is an integer, then
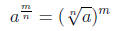
and
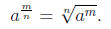
Example 0.2 Converting to
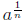
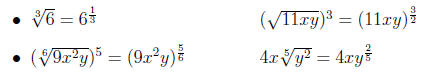
De nition 0.3 If
 is a nonzero real number , then
is a nonzero real number , then
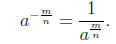
Example 0.3 Negative exponents
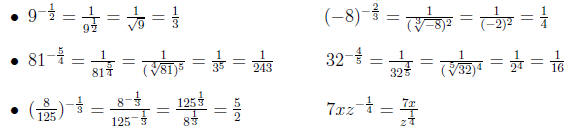
Property 0.1 Properties of Rational Exponents
If m and n are rational exponents , and a and b are real numbers for which
the following expressions are de ned, then
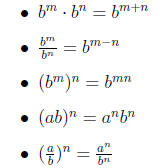
Example 0.4 Properties of Rational Exponents and Reducing
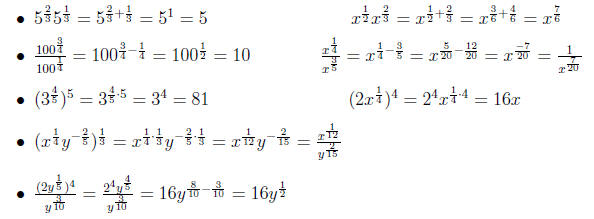
Property 0.2 Simplifying Rational Expressions
•Rewrite each radical expression with a rational exponent.
• Simplify using properties of rational exponents.
•Rewrite in radical notation .
Example 0.5 Simplify
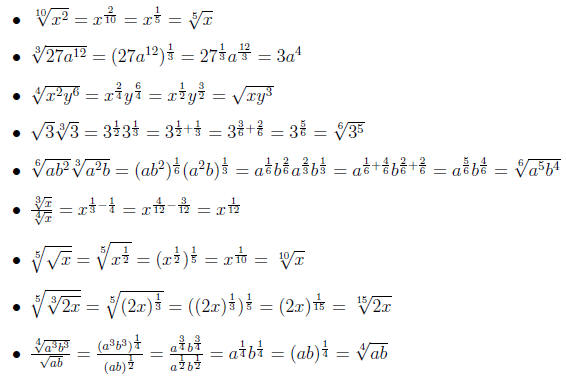
| Prev | Next |