Quadratic Functions and Models

Example: Graph the quadratic equation g(x) = 2x²-12x+ 23.

Solution Strategy : Find the vertex, the axis of symmetry, and determine a few points on the curve which we connect with a smooth curve.

Use the vertex formula : h = -b/(2a), k = g(h)
a = 2, b = -12, c = 23
h = -(-12)/(4) = 3
k = g(3) = 2(9) -12(3) + 23 so k = 18 –36 + 23 = 41 -36 = 5

Vertex at (3, 5).
Axis of symmetry: line x = 3

g(x) = 2x²-12x+ 23

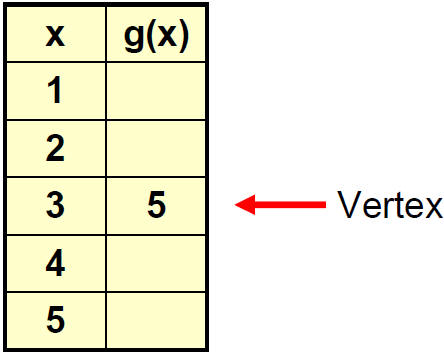
Vertex at (3, 5),
Axis of symmetry: line x = 3

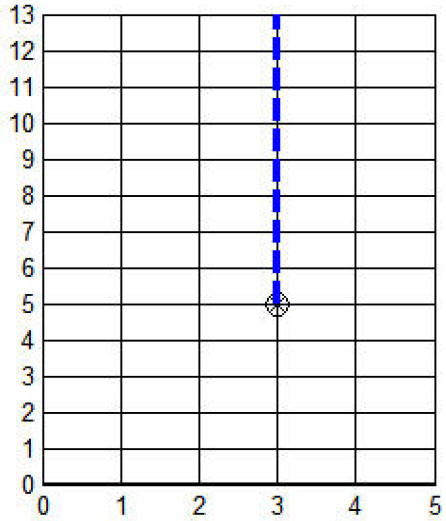
Since a = 2 > 0 the parabola opens upward.

g(x) = 2x²-12x+ 23

Vertex at (3, 5),
Axis of symmetry: line x = 3


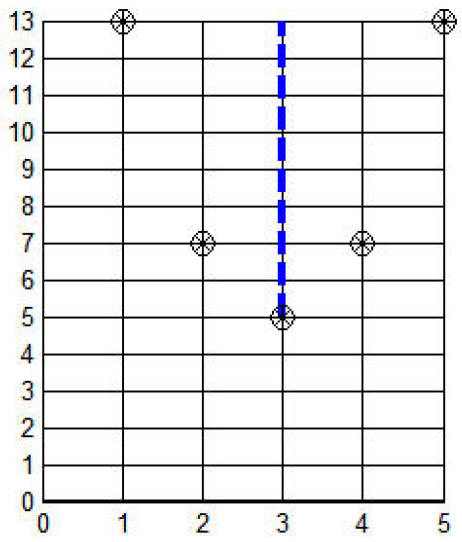
Since a = 2 > 0 the parabola opens upward.

Connect the points with a smooth curve.

g(x) = 2x²-12x+ 23

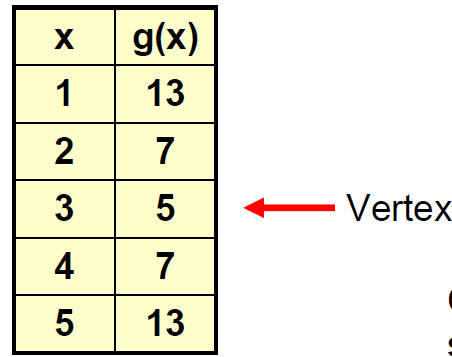
Vertex at (3, 5),
Axis of symmetry: line x = 3

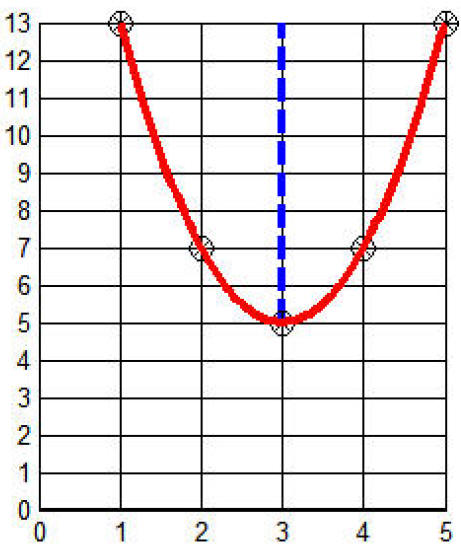
Since a = 2 > 0 the parabola opens upward.

Applications and Models Example

A junior horticulture class decides to enclose a rectangular garden, using part of the side of the greenhouse as one side of the rectangle. If the class has 32 feet of fence, find the dimensions of the rectangle that give the maximum area for the garden.

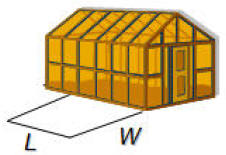
What do we want to find?
What requirements or constraints must we abide by?
What formulas will we be using?

Applications and Models Example continued

Find dimensions of rectangle.
We have 32ft of fence & the rectangle must have maximum area.

Area = length x width = L x W
Perimeter of the fence = distance around

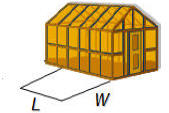
Because the 32-foot fence does not go along the greenhouse, it follows that
W + L + W = 32 or L= 32 –2W

The area of the garden is the length times the width. and we have L= 32 –2W.

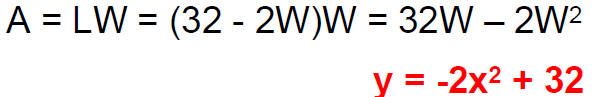
Here W plays the role of x and A plays the role of y

The area formula is a parabola that opens downward so the maximum value of the area occurs at the vertex. The vertex formula gives,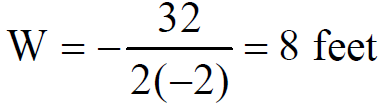
The corresponding length is
L= 32 –2W= 32 –2(8) = 16 feet.

The dimensions are 8 feet by 16 feet. So the maximum area of the garden will be A = 8×16 = 128 sq. feet.

A Common Situation :
A modeling process requires you to determine a maximum value or a minimum value. (For example maximum area or minimum cost, etc.) Such situations are called optimization or max/min problems.

If the equation that provides the math model is a quadratic f(x) = ax²+ bx+ c, then the value of x that is used to determine the optimal value is always at the vertex. That is,

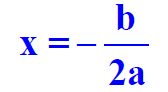
Example: Coyote airlines does a lot of charter business. They are running a special. The base fare is $250 (round trip to Las Vegas) but for a group of x ≥1 travelers the price is $(252 –2x). Determine the size of the group that will maximize the revenue for the charter flight.

Why this formula?

Step 1.Construct a function R(x) that computes the ticket revenue for a flight.
R(x) = x(252 –2x) = 252x –2x²
Step 2:Determine value of x that maximizes the revenue.

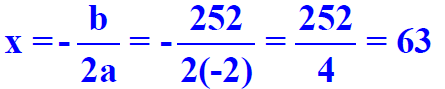
Step 3.Compute the maximum revenue.
R(63) = $7938

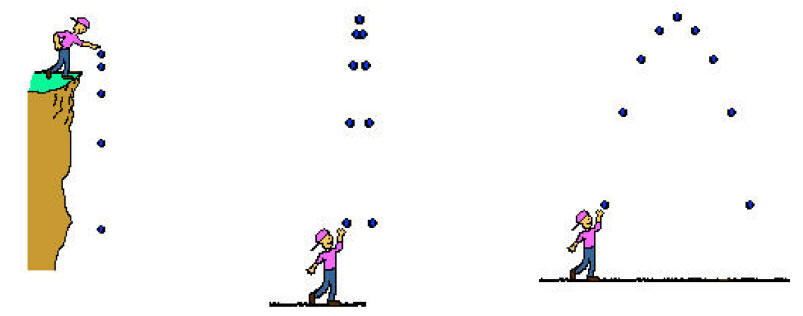
Projectile Motion: Discussion

A projectile is an object upon which the only force acting is gravity. There are a variety of examples of projectiles.

An object dropped from rest is a projectile (provided that the influence of air resistance is negligible).

An object which is thrown vertically upward is also a projectile (provided that the influence of air resistance is negligible).

An object which is thrown vertically upward is also a projectile (provided that the influence of air resistance is negligible).

An object is which thrown upward at an angle to the horizontal is also a projectile (provided that the influence of air resistance is negligible).

The equation that gives the height s of a projectile at time t is a quadratic function

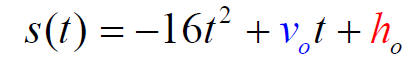
where v₀represents its initial velocity in feet per second, h₀represents its initial height in feet, and of course time t is measured in seconds.

The coefficient -16is related to the earth’s acceleration of gravity which is (about) 32 feet per sec per sec. The negative sign results from gravity acting as a downward force.

If the initial velocity is upward then v₀> 0(positive) and if it is downward then v₀< 0 (negative).

Projectile motion equation is

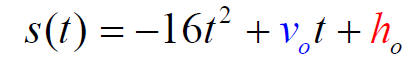
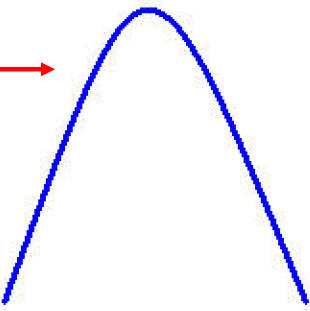
Since the coefficient of t ²is negative the parabola opens downward. This tells us that the projectile has its maximum height at the vertex (h, k) of the parabola.

h = time at which the maximum height occurs
k = the maximum height

The path of flight of a projectile looks like or a portion of this parabolic curve .

Example

A model rocket is launched with an initial velocity of v_o= 150 feet per second and leaves the platform with an initial height of h_o= 10 feet.

a) Write a formula s(t) that models the height of
the rocket after t seconds.
b) How high is the rocket after 2 seconds?
c) Find the maximum height of the rocket.

Solution:

(a)

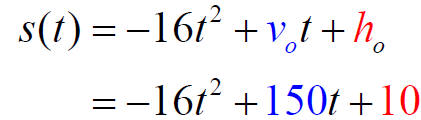
Solution continued:

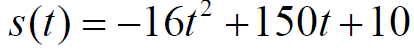
b) How high is the rocket after 2 seconds ?

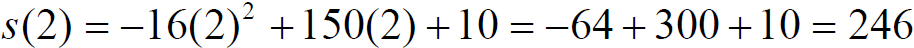
The rocket is 246 feet high after 2 seconds.

c) Because a is negative , the vertex is the highest point on the graph, with a t- coordinate of

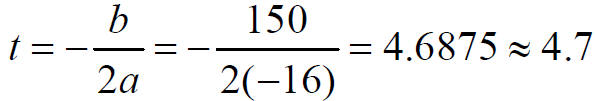
The y- coordinate is :

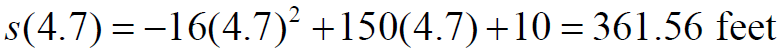
The vertex is at (4.7, 361.6).
So the rocket’s maximum height is (about) 361.6 feet.

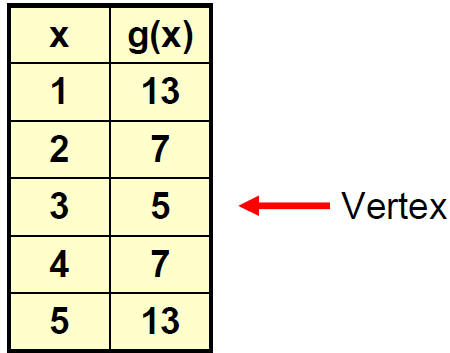
Example
A well-conditioned athlete’s heart rate can reach 200 beats per minute (bpm) during a strenuous workout. Upon stopping the activity, a typical heart rate decreases rapidly and then gradually levels off. See the data table.

Graphing this data we get

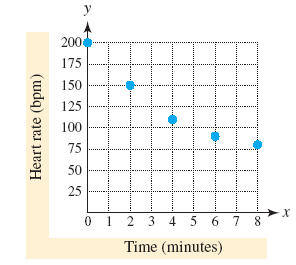
Determine the equation of a parabola that models this data.
f(x) = a(x–h)²+ k
How do we start?

From the description, we will take that the minimum heart rate is 80 beats per minute and that occurs when x = 8.
That means the vertex is at (8, 80).
So using the vertex form we have f(x) = a(x–8)²+ 80

How do we find the value of coefficient a?
a = 1.875

Example