Quadratic Equation

Let's begin by completing the square on a generic quadratic equation .

Example 0.1 ax² + bx + c = 0

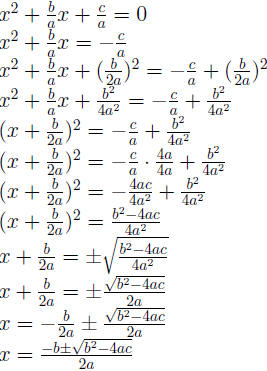
This formula allows us to skip the algebra and go straight to the solution.
That is for ax² + bx + c = 0,

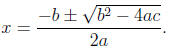
All we have to do is identify the values for a , b, and c in the quadratic
equation and substitute them into the formula we derived.

Example 0.2 Solve : x² + 8x + 15 = 0
a = 1 b = 8 c = 15
Using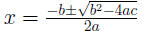

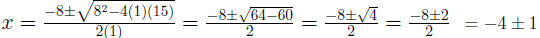
The solution set is { -5,-3}

Example 0.3 Solve : x² + 6x + 13 = 0
a = 1 b = 6 c = 13
Using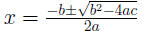

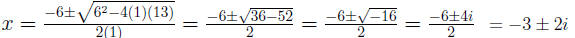
The solution set is { -3 ± 2i}

Example 0.4 Solve : 3x² = 4x - 6
so 3x² - 4x + 6 = 0
a = 3 b = -4 c = 6
Using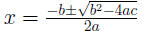

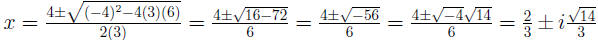
The solution set is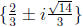

In the previous examples we could have solved x ² +8x+15 = 0 by factoring
over the real numbers . However, x² + 6x + 13 = 0 could not be solved this
way. How do we know when we will get real number solutions to an equation
and when we will get complex numbers as solutions?

Property 0.1 The discriminant of ax² + bx + c = 0 is b² - 4ac. Notice
that this is the part of the quadratic equation 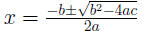that appears
under the square root .
So when the discriminant is positive then the solutions will be real numbers.
When the discriminant is negative the solutions will be complex numbers.

Remember that when we graph equations , the output corresponds to the
y-value of the graph. When we solve equations that are set equal to zero ,
we are really finding the x- intercepts . When solving quadratic equations,
ax² + bx + c = 0, we always get 2 solutions. But these solutions manifest in
different ways .

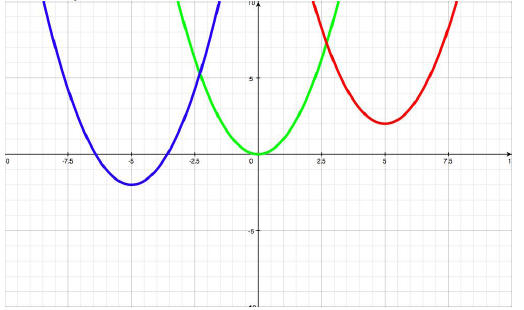
• The blue graph crosses the x-axis twice. This means that solving the
corresponding equation will give two distinct real numbers. For ex-
ample x² - 8x + 15 = (x - 5)(x - 3) = 0. This happens when the
discriminant is greater than 0.

• The green graph just touches the x-axis in one spot. This means the
graph has one real solution that is repeated. For example x²-10x+25 =
(x - 5)(x - 5) = 0. This happens when the discriminant is equal to 0.

• The red graph has no x-intercepts. It has 2 solutions but they are not
real numbers. For example x² + 1 = (x + i)(x - i) = 0. This happens
when the discriminant is less than zero.

Given a solution set we can write a quadratic equation that has the given
solution set.

Example 0.5 Write a quadratic equation with solution set { -2, 6}.

so x = -2 or x = 6
so x + 2 = 0 or x - 6 = 0
so (x + 2)(x - 6) = 0
so x² - 4x - 12 = 0

What is the solution set of 2(x + 2)(x - 6) = 2x² - 8x - 24 = 0?
What does this tell us?
For any real number a, a(x + 2)(x - 6) = 0 will have the same solution set.