Projection Methods for Linear Equality Constrained Problems
Projection Methods for Linear Equality Constrained Problems
4 Solving the Direction -Finding Problem (DFP)
Approach 1 to solving DFP: solving linear equations
Create the system of linear equations:
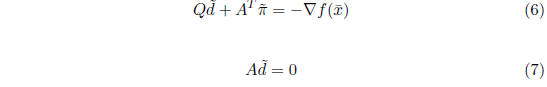
and solve this linear system for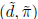
by any method at your disposal.
If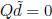 
, then
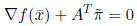
and so
is a Karush-Kuhn-Tucker point of P.
If 
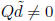, then rescale the solution as follows :
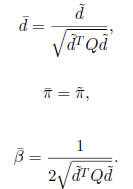
Proposition 4.1 
defined above satisfy (1), (2), (3), (4), and (5).
Note that the rescaling step is not necessary in practice,
since we use a
line-search.
Approach 2 to solving DFP: Formulas
Let
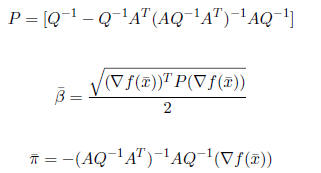
If
> 0, let
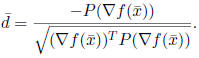
If
=0, let
=0.
Proposition 4.2 P is symmetric and positive semi-definite. Hence
≥ 0.
Proposition 4.3
defined above satisfy (1), (2), (3), (4), and (5).
5 Modification of Newton’s Method with Linear
Equality Constraints
Here we consider the following problem:
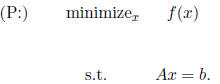
Just as in the regular version of Newton’s method, we
approximate the
objective with the quadratic expansion of f(x) at
:
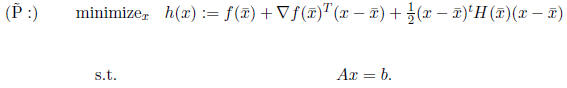
Now we solve this problem by applying the KKT conditions,
and so we
solve the following system for (x, u):
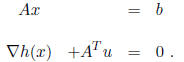
Now let us substitute the fact that:
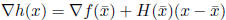and
.
Substituting this and replacing
, we have the system:
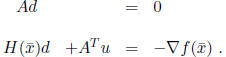
The solution (d, u) to this system yields the Newton
direction d at .
Notice that there is actually a closed form solution to this system, if we
want to pursue this route. It is:
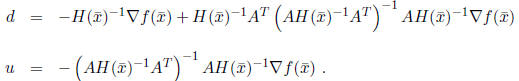
This leads to the following version of Newton’s method for
linearly
constrained problems:
Newton’s Method for Linearly Constrained Problems:
Step 0 Given x0 for which Ax0 = b, set k ← 0
Step 1 ← xk.
Solve for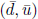 
:
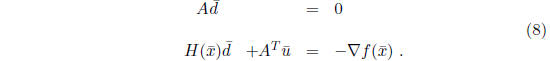
If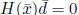 
, then stop.
Step 2 Choose step-size αk =1.
Step 3 Set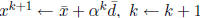 
Go
to Step 1.
Note the following:
• If , then
is a KKT point. To
see this, note from Step 1
that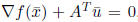 
, which are precisely the KKT conditions
for
this problem.
• Equations (8) are called the “ normal equations ”. They were derived
presuming that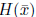 
is positive-definite, but can
be used even when
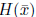is not positive-definite.
• If 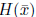is positive definite , then
is a descent
direction. To see this,
note that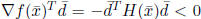 
from(8) since
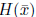is positive
definite.
6 The Variable Metric Method
In the projected steepest descent algorithm, the direction d must lie in the
ellipsoid
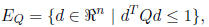
where Q is fixed for all iterations. In a variable metric
method, Q can
vary at every iteration. The variable metric algorithm is:
Step 1.
satisfies
Compute
.
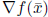Step 2. Choose a positive-definite symmetric matrix Q. (Perhaps
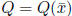
, i.e., the choice of Q may depend on the current point.) Solve the
direction-
finding problem (DFP):
DFP:
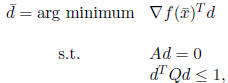
If
, stop. In the case,
is a KKT point.
Step 3. Solve
for the stepsize
, perhaps chosen by an
exact
or inexact linesearch.
Step 4. Set
Go to Step 1.
All properties of the projected steepest descent algorithm still hold here.
Some strategies for choosing Q at each iteration are:
• Q = I
• Q is a given matrix held constant over all iterations
• Q = where H(x)
is the Hessian of f(x). It is easy to show
that that in this case, the variable metric algorithm is equivalent to
Newton ’s method with a line-search, see the proposition below.
• 
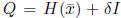, where 
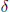is chosent to be large for early iterations,
but 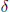is chosen to be small for later
iterations. One can think of this
strategy as approximating the projected steepest descent algorithm in
early iterations, followed by approximating Newton’s method in later
iterations.
Proposition 6.1 Suppose that Q =
in the variable
metric algorithm.
Then the direction in
the variable metric method is a positive scalar times
the Newton direction.
Proof: If Q = ,
then the vector of
the variable metric method is
the optimal solution of DFP:
DFP:
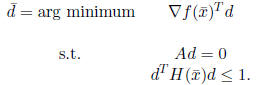
The Newton direction
for P at the point
is the solution of the following
problem:
NDP:
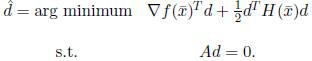
If you write down the Karush-Kuhn-Tucker conditions for
each of these two
problems, you then can easily verify that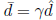 
for some scalar γ> 0.
q.e.d.
| Prev | Next |