Project 2 Solving Linear Systems
This project has two parts .
1. A Matlab function LowerSolve for solving lower triangular systems by
column oriented forward substitution
and the Matlab script TestLowSolve.m for testing LowerSolve are provided on the
course
web page. Modify LowerSolve to produce a Matlab function UpperSolve that solves
upper triangular
systems using row oriented backward substitution . Modify TestLowSolve.m to give
a Matlab script
TestUppSolve.m which compares the result of using both your function UpperSolve
and the Matlab
backslash operator on randomly generated upper triangular systems of sizes 4, 8
and 16.
You must submit printouts of TestUppSolve.m and UpperSolve.m, and the output
from running the
script TestUppSolve.m. Also, provide marked up listings of TestLowSolve.m and
LowerSolve showing
the changes that you made .
2. You are to compute solutions to systems of linear equations , to calculate
the errors in the computed
solutions, and to calculate the residuals for the computed solutions. Each
linear system has n equations
in the n unknowns x 1, x2, . . . , xn.
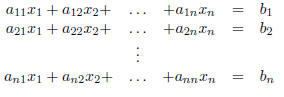
that is, in matrix vector form,
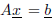where
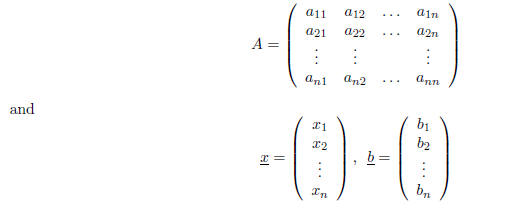
The matrix A is to be set to the Hilbert matrix of order n . Use the Matlab command hilb to build A.
For n odd, the right hand side, b , must be set so that the true solution to the linear system is
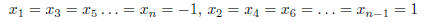
One way to form
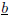is first to form
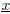using the above values, then to compute
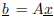using the simple
Matlab command
b = A * x
In a single program, for linear systems of size n = 6, 8, 10 and 12 in turn.
(a) Calculate the matrix A, the true solution
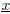and right hand side
.
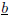(b) Find an approximate solution
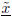of the linear system
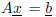using the Matlab backslash operator
to solve the linear systems, and print in a table the maximum magnitude of the
components of
the error
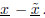
(c) Compute and print the maximum magnitude of the components of the residual
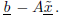
The Matlab script vande on the course web page may be of assistance as a template for this project.
To complete this part of the assignment, you must submit.
•A printout of the program that you used to compute the approximate
solutions, errors and
residuals.
•The output containing the approximate solutions, errors and residuals.
•A brief report outlining the problem and what you did to solve it. (Either give
a list of the
changes you made to vande or provide a marked up copy of vande showing your
changes.) Your
report should discuss the magnitudes of the errors and residuals, their behavior
as the value of n
increases , and the probable cause of their sizes.
| Prev | Next |