Notes on a^x and loga(x)
Here is an approach to the exponential and logarithmic
functions which avoids any
use of integral calculus. We use without proof the existence of certain limits
and assume
that certain functions on the rational numbers can be extended to continuous
functions on
the reals. All of this can be justified, but we do not do so here.
Let a be a positive real number . We want to define ax. For n a
positive integer, an
is a multiplied by itself n times. Similarly, a-n is a-1 multiplied by itself n
times. Every
positive number has a unique positive m- th root , so we can define (for m a
positive integer)
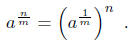
Having defined ax for x a rational number, we define ax
for all real x by choosing a sequence
of rationals converging to x, etc. This process leads to a well defined function
ax which is
a continuous function from the whole real line to the positive reals.
Proposition 1.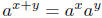 
and
. Moreover, a0 = 1 and a1 = a.
Proof. The first two assertions follow by first proving them for x and y
rational and then
using continuity. To show a0= 1, set x and y both equal to 1 in the second
identity. That
a1 = a follows from the definition.
Lemma 2. Assume a > 1. Then ax is a strictly increasing function.
Proof. Suppose x < y and that x and y are rational. By adding a positive integer
to both
sides, we can assume that x and y are positive. Write both over a common
denominator
N. Thus, x = m/N and y = n/N. Since x < y, we have m < n. Now, a > 1 implies
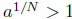. Thus,
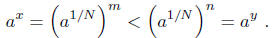
Having established the result for rational numbers, the
general result follows by taking
limits.
Definition. For a > 0, the limit
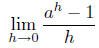
exists. It is called ln(a), the natural logarithm of a.
Proposition 3. The derivative of ax exists, and we have
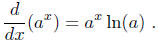
Proof. This follows easily from the definitions
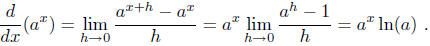
Remark: note the above proposition is similar to how we differentiated trigonometric
functions. To find the derivative of sin(x) or cos(x) at any point, we needed to
compute
two limits ,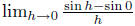
and
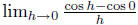, the derivative of sine and cosine at any
point followed by the angle addition formulas . Here, the analogue is
.
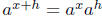Corollary. If a > 1 then ln(a) > 0. For a = 1, ln(1) = 0. If 0 < a < 1, then
ln(a) < 0.
Proof. The second assertion is clear since 1x = 1 for all x and so its
derivative is zero.
To prove the first assertion, note that if ln(a) < 0 the by the Proposition, ax
is
decreasing. This contradicts Lemma 2. Thus, ln(a) ≥ 0 if a > 1. However, it
can't be 0,
since then the derivative of ax would be identically zero by Proposition 3, and
ax would be
a constant. This again contradicts Lemma 2. Thus, ln(a) > 0. Finally, if a < 1,
we have
ax = ((a-1)x)-1 is decreasing, so, by repeating the reasoning above, we find ln(a) < 0.
Remark: We do not consider ln(a) for a ≤ 0.
Proposition 4. Assume a, b > 0. Then ln(ab) = ln(a) + ln(b).
Proof. By definition,
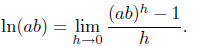
As
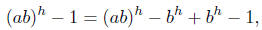
we have
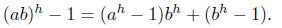
Therefore
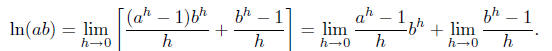
As h → 0, note bh → 1, and we therefore find that
log(ab) = ln(a) + ln(b).
Then, ln(ab) = ln(a) + ln(b) .
Proof. We have already proved the first assertion, but here is a second proof
using
Proposition 4.
ln(1) = ln(1 · 1) = ln(1) + ln(1),
which implies ln(1) = 0.
Now, 0 = ln(1) = ln(a · a-1) = ln(a) + ln(a-1). The second assertion follows.
Lemma 5. ln(x) is a strictly increasing function.
Proof. Suppose 0 < x < y. Then, 1 < y/x and ln(y/x) > 0 by the Corollary to
Proposition 3. Thus ln(y) - ln(x) > 0, or ln(x) < ln(y), which proves the
assertion.
Proposition 6. For all positive a, we have ln(ax) = x
ln(a) .
Proof. Let f(w) = ln(ax). Using Proposition 4, one easily
checks that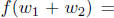 
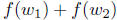. By simple algebra one deduces that
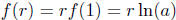for all
rational
numbers r. Since f(w) is continuous, the Proposition follows for all real
numbers x.
Corollary. As x → ∞, ln(x) → ∞. Also, as x → 0, ln(x) → -∞.
Proof. Since ln(x) is increasing we only have to prove that it takes on
arbitrarily large
values as x gets bigger and bigger. Consider the sequence
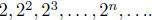We have
ln(2n) = n ln(2) → ∞ as n → ∞.
Similarly, on the sequence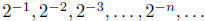 
we have
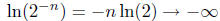as n → ∞ .
This completes the proof.
Definition. The following limit exists
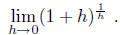
We call this limit e, Euler's constant, e is approximately
2.71828. Note that another
expression for e is given by
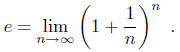
Proposition 7. The function ln(x) is differentiable. We have
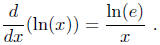
Proof. As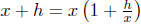 
, using
Proposition 4 we have
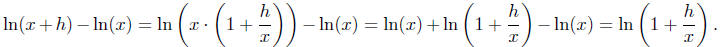
Therefore we have
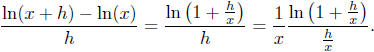
Using the definition of the derivative, we see that
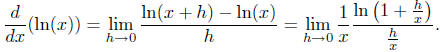
Letting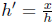 
, as h → 0 we
see h' → 0. By Proposition 6,
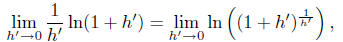
and by the above definition this limit is just ln(e).
Combining the pieces gives the derivative
of ln(x) is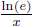 
, as claimed.
Proposition 8. ln(e) = 1 .
Proof. By Proposition 6, we have
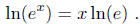
Differentiate both sides using what we have proven and, of course, the chain
rule.
Remember that e is a constant, so ln(e) is just a number { it has no x
dependence. Thus,
the derivative with respect to x of ln(e) is zero , and the derivative with
respect to x of
x ln(e) is thus ln(e).
We use the chain rule to differentiate ln(ex). Let f(x) = ln(x) and let g(x) =
ex.
Then ln(ex) = f(g(x)), so by the chain rule its derivative is f'(g(x))
· g'(x).
We get the
derivative of f from Proposition 7, and the derivative of g from Proposition 3.
Substituting
gives
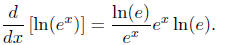
We have shown that this derivative is also equal to ln(e),
therefore we find that [ln(e)]2 =
ln(e). Since ln(e) ≠ 0, we must have ln(e) = 1.
Corollary.
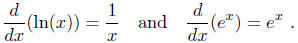
Definition. We define the logarithm function to the base a by the following formula
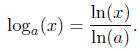
This function has all the properties one would expect. We
list them. The proofs are
very easy and are left to the reader.
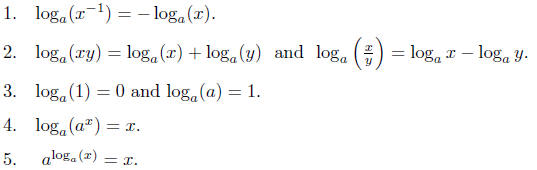
6.
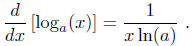
7. If a > 1, then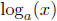 
is strictly increasing and its
graph is everywhere concave down.
It goes to ∞ as x → ∞ and to minus ∞ as x → 0.
Finally, we note that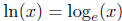 
, so that we have
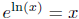and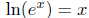 
.
What this means is that if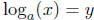 
then x = ay. In other words,
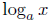is
the number
of powers of a we need to get x.
For example, consider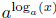 
: we raise a to the number of powers of a we need
to
get x, thus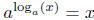 
.
Finally, note that in general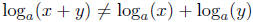
, the logarithm of
a sum
is not the sum of the logarithms.
| Prev | Next |