Negative Exponents Practice Questions
1. Write 7 × 7 × 7 × 7 × 7 using exponents.
2. Write a × a × a ×b × b × b× b × b using exponents.
3. Write 22m3without using exponents.
4. Simplify and write without negative exponents:

5. Simplify and write without negative exponents :
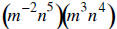
6. Simplify and write without negative exponents:
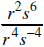
7. Simplify and write without negative exponents:

8. Simplify each and write without negative exponents:

9. Simplify and write without negative exponents: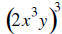
10. Simplify and write without negative exponents:
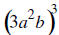
11. Simplify and write without negative exponents:
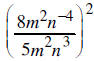
12. Simplify and write without negative exponents: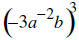
13. Simplify and write without negative exponents:
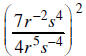
14. Simplify and write without negative exponents:
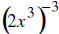
15. Write each number in scientific notation.
(a) 52,000
(b) 0.000000076
(c) 0.00000067
(d) 250,000
16. (a) Multiply using scientific notation and exponent rules and write your
answer in
scientific notation.
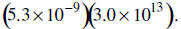
(b) Write your answer above without exponents.
17. (a) Divide using scientific notation and exponent rules and write your
answer in
scientific notation.
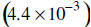 divided by (2 ×105 )
divided by (2 ×105 )
(b) Write your answer above without exponents.
18. Astronomers measure large distances in light-years. One light year is the
distance
that light can travel in one year and is 5,880,000,000,000 miles. A star is
determined to
be 8.5 light years form Earth. Express the distance to the star in miles using
scientific
notation.
19. In 1996 the national debt was $5,200,000,000,000 and the population of the
U.S. was
about 260,000,000 people. To the nearest dollar, what was each person’s share of
the
debt?
20. Tell if each is a monomial , binomial, trinomial or not a polynomial.
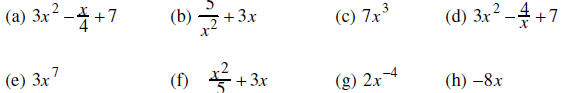
21. Put each polynomial in descending order and state the degree.
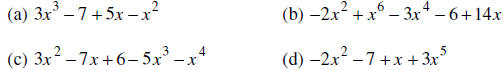
22. ADD :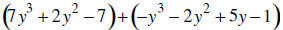
23. SUBTRACT : 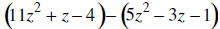
24. ADD: 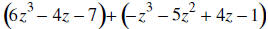
25. SUBTRACT: 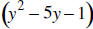 from
from
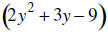
26. MULTIPLY: 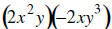
27. MULTIPLY: 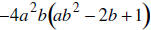
28. MULTIPLY: (3x − 5)(7x + 4)
29. MULTIPLY: 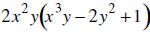
30. MULTIPLY: 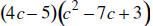
31. MULTIPLY: (5z + 2)(5z − 2)
32. MULTIPLY: 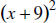
33. MULTIPLY: (2x − 5y)(2x + 5y)
34. MULTIPLY: 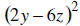
35. DIVIDE: 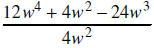
36. DIVIDE using long division: 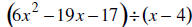
37. DIVIDE 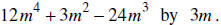
38. DIVIDE using long division: 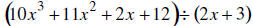
39. Show that 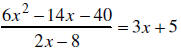 by checking the division. (Don’t just re-do the
by checking the division. (Don’t just re-do the
division.)
40. DIVIDE using long division:
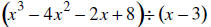
41. Find the GCF ( greatest common factor) of 4 and 6.
42. Find the GCF of 28, 104, and 76.
43. Find the GCF of the terms 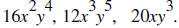
44. Find the GCF of the terms 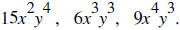
45. Factor the greatest common factor: 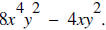
46. Factor the greatest common factor: 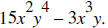
47. Factor the GCF: 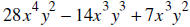
48. Factor by grouping: 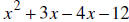
49. Factor by grouping: ac + ad + bc + db
50. Factor completely: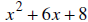
51. Factor completely:
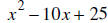
52. Factor completely: y 2– 7 y – 18
53. Factor completely: y2 + 5y – 10
54. Factor completely: 4x2 + 16x – 20
55. Factor the difference of two squares : 
56. Factor the difference of two squares : 
57. Factor the difference of two squares: 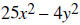
58. Factor completely: 3x2 – 12x – 15
59. Factor completely: x2+ 25
60. Factor the perfect square trinomial: y2+12y + 36
61. Factor the perfect square trinomial: z2− 4z + 4
62. Write this quadratic equation in standard form. 2x = 5 – 3x2
63. Write this quadratic equation in standard form. 5x – 2x2= 4
64. Is the equation −3x2+ 3x + 2 = −4 a quadratic equation? Why or why not?
65. Is the equation 3x + 2 = −4 +12x a quadratic equation ? Why or why not?
66. What do you know about c and d if c × d = 0 ?
67. Solve for x : x(x + 3) = 0
68. Solve for x: (x − 2)(x + 5) = 0
69. Solve for x by factoring: 64x = x2
70. Solve for x by factoring: x2– 7x –18 = 0
71. Solve for x by factoring: x2– 5x – 24 = 0
72. Solve for x by factoring: x2– 9x + 20 = 0
ANSWERS for Unit #4 Practice Questions
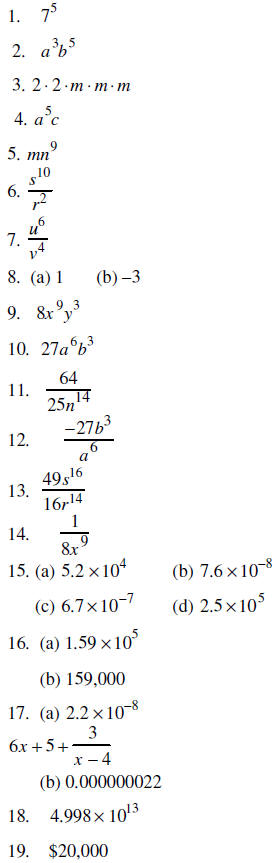
20.
(a) trinomial (b) not a poly
(c) monomial (d) not a poly
(e) monomial (f) binomial
(g) not a poly (h) monomial
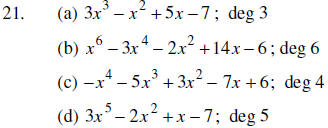
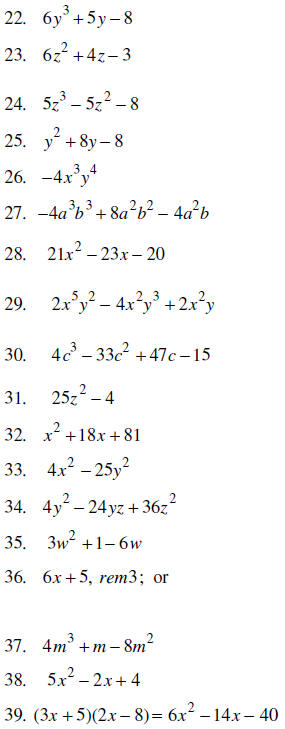
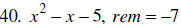
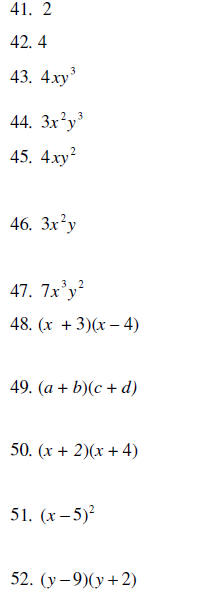
53. can’t be factored
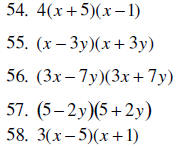
59. Can’t be factored
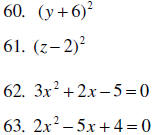
64. Yes, because it has an x2 term
65. No, it is linear
66. Either c = 0 or d = 0
67. x = 0 or x = –3
68. x = 2 or x = – 5
69. x= 0 or x = 64
70. x = 9 or x = –2
71. x = 8 or x = – 3
72. x = 4 or x = 5
| Prev | Next |