Math Homework Problems
TERMS YOU SHOULD KNOW : the number of divisors of a number , gcd’s,
lcm’s.
1. Find the number of divisors of each of the following numbers. Note: You
don’t have to find the divisors themselves . Some of these numbers look
remarkably similar to some in the last section.
(a) 21
(b) 21,000
(c) 26,460
(d) 1,000,000
(e) 3,000,000
(f) p111, where p is prime.
(g)
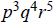 ,
where p, q, and r are all prime.
,
where p, q, and r are all prime.
(h)
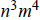 ,
where n and m are any positive integers .
,
where n and m are any positive integers .
2. A number has exactly 18 divisors.
(a) What are the possible forms of its prime factorization ?
(b) What is the smallest number with exactly 18 divisors?
(c) What is the largest number with exactly 18 divisors?
3. Find the least common multiple (lcm) and the greatest common divisor
(gcd) of each pair of numbers.
(a) 21 and 14
(b)
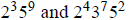
(c) 1,000,000 and 3,000,000
(d) 1 and n, where n is any positive integer .
(e)
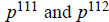 ,
where p is prime.
,
where p is prime.
(f)
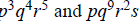 ,
where p, q, r, and s are all prime.
,
where p, q, r, and s are all prime.
(g) 21,000 and 26,460
1a. Since 21 = 3 · 7, this has (1+1)(1+1) = 4 divisors.
1b. Since 21,000 =
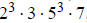 this has (4)(2)(4)(2) = 64 divisors.
this has (4)(2)(4)(2) = 64 divisors.
1c. Since 26,460 =
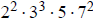 ,
this has (3)(4)(2)(3) = 72 divisors.
,
this has (3)(4)(2)(3) = 72 divisors.
1d. Since 1,000,000 =
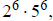 this has (7)(7) = 49 divisors.
this has (7)(7) = 49 divisors.
1e. Since 3,000,000 =
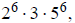 this has (7)(2)(7) = 98 divisors.
this has (7)(2)(7) = 98 divisors.
1f. 111+1 = 112.
1g. (4)(5)(6) = 120.
1h. Since we don’t know if n and m are prime, there is no way to know how
many divisors
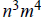 has.
has.
2a. Well, 18 = 2·32, so we can figure out the different ways to partition one
2 and two 3’s:
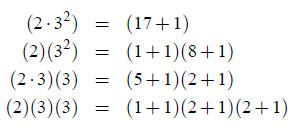
So, using the formulat for d (n) and the partitions above,
the four possible
prime factorizations of a number with exactly 18 divisors are, respectively,
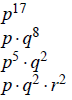
2b. Using the previous answer , just plug in the smallest
possible primes into
each form and see which gives the smallest number. So, we compare
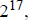
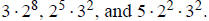 The smallest is the last one, which equals
180.
The smallest is the last one, which equals
180.
2c. There is no such largest number, since there is no largest prime.
3a. Since 21 = 3 · 7 and 14 = 2 · 7, their lcm is 2 · 3 ·
7 = 42 and their gcd is
7.
3b. Their lcm is 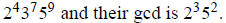
3c. Since 1,000,000 divides 3,000,000, their lcm is
3,000,000 and their gcd
is 1,000,000.
3d. Their lcm is n and their gcd is 1.
3e. Since 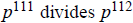 , their lcm is
, their lcm is
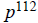 and their gcd is
and their gcd is
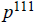 .
.
3f. Their lcm is 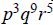 and their gcd is
and their gcd is
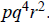
3g. Since 21,000 = 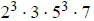 and 26,460 =
and 26,460 =
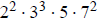 , their lcm is
, their lcm is
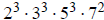 and their gcd is
and their gcd is
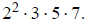
| Prev | Next |