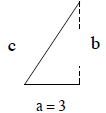Looking For Pythagoras

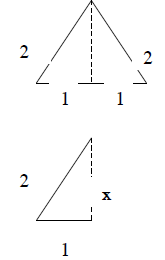
The sides of this 30-60-90 triangle satisfy the
Pythagorean relationship and so,

1² + x² = 2², so
x² = 3, so
x = √3.

The side lengths are 1, √3, 2 units

10. Triangle ABC, sketched below, has angles
30, 60, 90 degrees, and the shortest side length
is 3 units. What are the other side lengths?

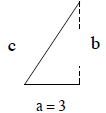
This triangle is a scaled up similar copy of the
triangle in example 9. (See Stretching and
Shrinking.) The scale factor is 3. So, the
lengths are 3(1), 3(√3), and 3(2) units, or 3,
3√3, 6 units.

11. Triangle PQR is a 45-45-90 triangle. The
hypotenuse is 5 units long. How long are the
other sides?

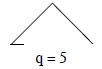
The ratio of side lengths for a 45-45-90 triangle
is 1:1:√2. In this triangle, which is a similar
copy of every other 45-45-90 triangle, the ratio
is p: r: 5, where p and r are the equal sides. We
can think of using a scale factor of 5/(√2) to
scale up a triangle with sides that measure 1, 1,
√2 units. This will create a triangle with sides
that measure 5/(√2), 5/(√2), 5 units, or
approximately 3.5, 3.5, 5
(Note: students could also find the sides by
using some algebraic reasoning .

P² +r² = q², so
p² + p² = 25, so
2p² = 25, so
p² = 12.5, so
p = √12.5. or approximately 3.5 units.)
q = 5
 

Note: every rational number can be written as a
decimal, either terminating or repeating . (See
Vocabulary, Bits and Pieces III.)
 

Irrational numbers: are numbers that can NOT be
written in the form a/b where a and b are integers.
Non-repeating, non-terminating decimals, and square
roots that do not work out exactly and ⇐ are examples
of irrational numbers.

Note: since numbers like √2 and √5 are irrational any
decimal approximation will be inexact, no matter how
many decimal places we use. √2 = 1.4142… and
√5 = 2.2360… The decimal approximations never
terminate and never repeat. If they did terminate or
repeat then these decimals could be written as
rational numbers; but √2 and √5 are irrational
numbers. Using the format √2 is exact, whereas
1.4142 is a very accurate, but inexact, approximation.
 

Real #’s: are all the numbers which are either
rational or irrational.

Note: every number that students know about at this
stage is a real number . In High School they will meet
other kinds of numbers, such as complex numbers .

ALL of these numbers are rational. They CAN
all be written as a/b.
2 = 2/1
2.4 = 24/10 (every terminating decimal can be
written as a fraction with a power of 10 for a
denominator )
0.1111… = 1/9 (see below)
-9 = -9/1
2 1/3 = 7/3
17/5 is already in the “a/b” format.
-2/7 is already in the “a/b” format.
From the above examples we can conclude that
any integer, any positive or negative fraction , or
mixed number, and any terminating decimal can
be written as a rational number.

13. a. Write 1/9 as a decimal.
Every fraction can be thought of as a division .
So 1/9 can be thought of as 1 ÷ 9. We can set
this up as a division, 1.0000 ÷ 9, and get the
decimal answer, 0.1111… (See Bits and
Pieces III for decimal division.)

b. Write 0.121212…as a rational number.
We can think of this as an algebra problem.
X = 0.121212…
So, 100x = 12.121212…
So, 100x – x = 12.121212…. – 0.121212….
= 12.
(Notice there is no repeating part now.)
So, 99x = 12. So, x = 12/99.
This strategy could have been used for any
repeating decimal. Any repeating decimal can
be written as a rational number.

14. Give an example of a non-terminating and
non-repeating decimal.
0.3 is a terminating decimal. 0.333…is a
repeating decimal. But 0.32332333233332…
has a pattern which neither terminates nor
repeats. Thus 0.32332333233332…is an
irrational number.