Lines and Linear Equations
By a linear equation we mean an equation of the form
y = ax + b (1)
where
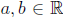 .
The distingushing feature is the single power of the variable x . A linear
.
The distingushing feature is the single power of the variable x . A linear
equation represents a line, that is the equation determines points in the plane
which we
can connect with a straight line. Moreover, given the graph of a line we can
write down its
(linear) equation. This requires two ingredients: the slope of the line and its
y-intercept.
The slope represents the change along the line along the y-axis versus the
change along
the x-axis. Given two points in in the plane (x1, y1) and (x2, y2) the slope of
the line
through them is found by computing
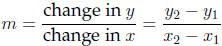 (2)
(2)
Example Find the slope of the line passing through the points (0, 1) and (−1,
1).
Let (x1, y1) = (−1, 1) and let (x2, y2) = (0, 1). Then
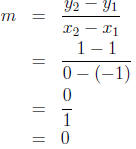
Therefore, the slope of the line through the points (0, 1) and (−1, 1) is m = 0.
The letter m is commonly used for the slope of a line, thus equation (1) becomes
y = mx + b (3)
Whenever a linear equation has the above form we say that is is in the
slope- intercept form .
Warning It is important to designate a start- and an end-point in slope
computations. In
the above example the same answer is obtained when (x1, y1) = (0, 1) and let
(x2, y2) =
(−1, 1). A common mistake is to take the points out of order .
Lines parallel to each other have the same slope, while lines perpendicular to
each
other have slopes which multiply to −1. That is, if m1 and m2 are the slopes of
two
perpendicular lines, then m1 ·m2 = −1. In other words, to find the slope of a
line perpendicular
to a given line one needs to find the negative reciprocal of the given slope. We
will
use the superscript ? to denote perpendicular slopes.
Example Find the slope of a line perpendicular to the line given by y = 3x + 1.
From the slope-intercept form of the line we read off the slope. We have m = 3
and
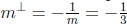 .
.
Horizontal lines have a zero slope . These line have the form y = c for some real
number c. The line in the first example is a horizontal line with equation y =
1. Vertical
lines are of the from x = k, where k is any real number . Vertical lines are
perpendicular to
horizontal lines, however, their slopes do not multiply to −1. This is because
vertical lines
have undefined slope: on a vertical line the change along the x-axis between
consecutive
points is 0, thus in the process of computing the slope of a vertical line we
would be
dividing by 0.
Example Find the equation of a line perpendicular to the line in the first
example.
We already know that the equation of the line is y = 1. From this equation we
read off
the slope (the coefficient of x ) to be 0. We cannot take the negative reciprocal
without
dividing by zero, but any vertical line will be perpendicular to y = 1. We can
choose
x = 1. The lines y = 1 and x = 1 are perpendicular and intersect at the point
(1, 1).
The final ingredient in determining the equation of a line is the y-intercept.
This is
the point where the graph of the line intersects the y-axis (the line x = 0) and
is obtained
by letting x = 0 in the line’s equation. In the above example x is identically
0, thus the
y-intercept is b = 1. In general, y-intercepts have the form (0, p). Similarly,
the x-intercept
is the point on the graph of the line which intersects the x-axis (the line y =
0) and is
obtained by letting y = 0 in the line’s equation. x-intercepts have the form (q,
0).
Example Find the equation of a line parallel to the line 5x + y = 7 and passing
through the
origin.
Writing the equation in slope-intercept form we have y = −5x + 7. We read off
the slope
to be m = −5. A parallel line will have the same slope and since the parallel
line must
pass through (0, 0) the y-intercept is b = 0. Therefore, the desired equation is
y = −5x.
It is possible to write down the equation of a line without explicitly
calculating its
y-intercept (see exercise 7). The point-slope form of a line through a point
(x1, y1) is
y − y1 = m(x − x1) (4)
Here the y-intercept is disguised as b = y1 − mx1.
Systems of Linear Equations
Given two or more linear equations we call the point (if one exists) where all
the lines
intersect the solution to this system of linear equations. In a previous example
we saw
that the lines x = 1 and y = 1 intersect at (1, 1). In other words, the solution
to the system
of equations
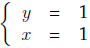
is the point (1, 1).
Example The y-intercept of the line y = mx+b is the solution to the system of
equations
given by
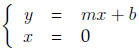
and the x-intercept is the solution to
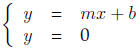
Example The solution to the system of equations
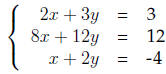
is the point (18,−11).
The main methods of solving a system of linear equations are elimination and
substitution .
When it is easy enough to solve for one variable , as in the example with the
x-intercept, we do so and then make a substitution in the other equation,
thereby obtaining
an easy to solve linear equation in one variable. Remember that multiplying both
sides of an equation by a number does not change the equation. To solve the
system
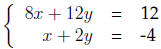
by elimination we would first multiply the bottom equation by -6 and obtain the
equivalent
system
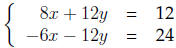
Adding both equations eliminates the variable y and we have 2x = 36 whence x =
18. It
then follows that y = −11 and therefore the solution to the system is (18,−11).
Note It is absolutely vital to check you answer by making sure that it is the
solution to
every equation.
| Prev | Next |