Linear Inequalities in Two Variables
A. A linear in two variables will look like:
Ax + By ≤ C
Ax + By < C
Ax + By ≥ C
Ax + By > C
B. The boundary line for a linear inequality will be:
1. Dotted for < or > (i.e. – no equality)
2. Solid for ≤ or ≥
C. The solution for a linear inequality is the set of all points that will make the inequality a true statement.
II. Graphing Inequalities
A. Procedure
1. Determine the boundary line and graph it.
2. Pick a checkpoint – a point that is clearly, obviously – not on the boundary line.
3. Substitute the values for x and y into the original
inequality and simplify . If you get:
a. A true statement, shade the side of the line that the checkpoint is on.
b. A false statement, shade the other side of the line.
B. Examples – Graph each inequality .
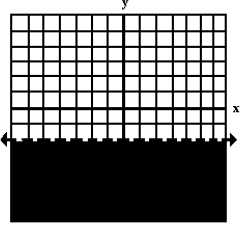
1. y < −2
First, we see that there is no equality involved, so the boundary line is
dotted .
Next, the boundary line is found by replacing the “<” with “=”, which in this
case will give us a boundary line of:
Boundary Line is y = −2.
Now we graph this line. We know from our previous discussions that this is a
horizontal line.
We now pick a checkpoint. The point (0, 0) looks pretty good ! Substituting into
the original inequality, we get:
0 < −2
This statement is false, so we shade the side of the line that is opposite of
the point (0, 0).
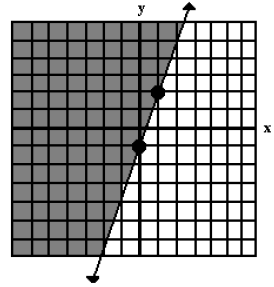
2. y ≥ 3x – 1
First, we notice that equality is involved here, so our boundary line is solid .
Boundary Line: y = 3x – 1
We next notice that this line is in slope-intercept form, so we can use our
knowledge of that to graph this boundary line.
m = 3, b = −1
So we will plot the point (0, 1), then rise 3, run 1 to get a second point.
Finally, we need to choose a checkpoint. Again, (0, 0) looks pretty good .
Substituting 0 in for x and 0 in for y in the original inequality, we get:
0 ≥ 3(0) – 1
OR
0 ≥ 0 – 1
OR
0 ≥ −1
This is true, so we shade the side of the line that the checkpoint is on.
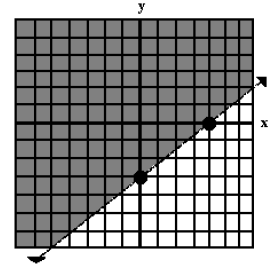
3. Now you try one: 3x – 4y < 12
| Prev | Next |