Inverse Functions and Their Derivatives, Including Logs and Trig
It’s time for us to find our last differentiation rules .
We now focus on the inverses of functions. To
understand inverses, though, we have to recall another
Definition. Recall that a function f is said to be a if any two different
inputs for
f give different outputs ; that is,
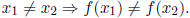
We can test whether or not a function is___ using the
___ Line Test . A function f___ is if and only if every ___passes
through the graph of f at most once.
Examples. Demonstrate that f (x) = x3 ___is but g (x) = x2 is not, both
algebraically
and using the ___Line Test.
Now what are we going to do with these one-to-one
functions?
Definition. If f is a one-to-one function, its inverse, written f -1, is defined
by
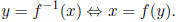
In this case we get cancellation rules :
f (f -1(x)) = x and f -1(f(y)) = y
whenever these compositions make sense.
Examples.
(1) The one-to-one function f (x) = x3 has what inverse? Graph them both on the
same axes
below:
(2) The function f (x) = ex has what inverse? Graph them both on the same axes
below:
(3) The function f (x) = x2 is only one-to-one if we restrict its domain to
[0,∞). In this case,
what’s f -1? Graph both the function f and its inverse on the same axes below.
The examples above suggest the following fact:
Observation. If f is a one-to-one function, the graph of the inverse y = f
-1(x)
is obtained by
reflecting the graph of y = f (x) over the line y = x. Moreover, the domain of
the inverse is the
range of the original function, and vice versa.
This shouldn’t be surprising: after all, the taking the inverse of a function
merely exchanges the
roles of x and y.
But what about derivatives? Let’s use the Chain Rule to
figure out how to differentiate f -1(x).
Start with y = f -1(x). Thus x = f (y). Differentiating this equality implicitly,
what do you get?
Now, just as we did with implicit differentiation before , solve for
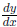, since that’ s really (f -1)'(x).
What do you get? Write your answer proudly below and circle it ; it’ll be useful!
Specific examples. Applying our newfound method for finding the derivative of an
inverse
function, we can now obtain the following formulas :
(1) Let y = ln(x), so x = ey. Here f (y) = ey. What formula do we obtain for
?
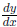(2) Since the function sin (x) is not one-to-one, we must
restrict its domain, much as we did for
x2 before. Let’s agree to restrict the domain to
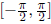. Draw a graph below showing how
on this new domain sin (x) is indeed one-to-one:
What about the derivative of the inverse sine (or ___)
function, sin-1(x)? Let
y = sin-1(x). Now find 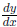, rewriting it in terms of x at the end:
(3) Similarly, we may restrict the function cos (x) to the domain [0, π] in order
to ensure that it
is one-to-one. Here’s some room to draw a graph of the inverse cosine (or
___)
function y = cos-1(x) and come up with a formula for
:
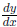(4) Lastly, let’s do tan(x), restricting its domain
to 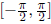to make sure it’s one-to-one.
What derivative do you come up with for the inverse tangent (or ___) function,
tan-1(x)?
Homework. The following exercises are due on Friday, May
1st, but if you turn them in to me
by Friday, April 24th, I’ll be sure to grade them and get them back to you
before Exam 3.
(1) Find the derivative of each of the following functions.
(
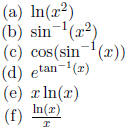
(2) Just to get some practice with some of the more important inverse functions,
give values
for the quantities indicated below.
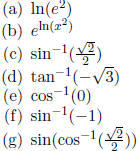
(3) Analyze the function f (x) = x ln (x) as carefully as you can using the first
derivative (to
test for extrema and increasing/decreasing behavior), the second derivatives (to
test for
concavity), and asymptotes.
(4) Repeat (3) with the function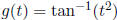 
.
(5) Note that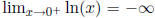 
and
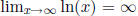. You may use these facts
without
proving them, in order to calculate the following limits. (Hint:
the
first couple!)
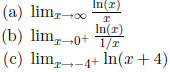
| Prev | Next |