Hyperbolic Trigonometric Functions

Just as trigonometry can be performed on the unit circle , it can also be performed on the unit hyperbola :

x² − y² = 1.

Define the hyperbolic cosine function by



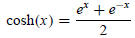
and the hyperbolic sine function by



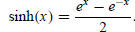
A simple computation then shows that

cosh²(x) − sinh²(x) = 1,

which is the hyperbolic trigonometric identity analogous to the Pythagorean identity

cos²(x) + sin²(x) = 1

from ordinary (circular) trigonometry.

Next, as in the case of ordinary trigonometry , we define the remaining four hyperbolic trigonometric functions
from these first two :

Define the hyperbolic tangent function by



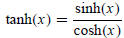
and the hyperbolic cotangent function by



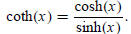
Define the hyperbolic secant function by



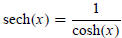
and the hyperbolic cosecant function by



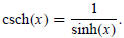
Hyperbolic Pythagorean Identities

In addition to the identity derived earlier,

cosh²(x) − sinh²(x) = 1,

there are two other hyperbolic identities obtained by dividing this one by sinh²(x) and cosh²(x), respectively:

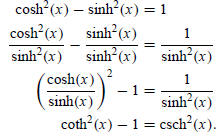
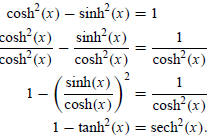
We summarize these here:

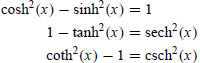
Derivatives of Hyperbolic Functions

By using the definition of the hyperbolic sine function, we have

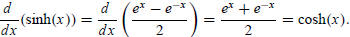
Similarly,

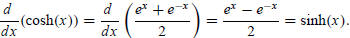
The derivatives of the remaining hyperbolic trigonometric functions are obtained from their definitions using the
Pythagorean hyperbolic trigonometric identities , the definitions of the hyperbolic functions, and the quotient rule :

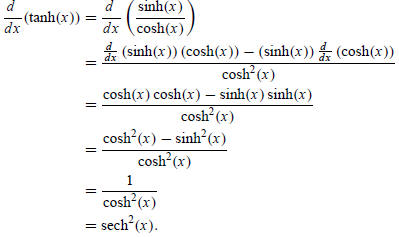
Similarly,

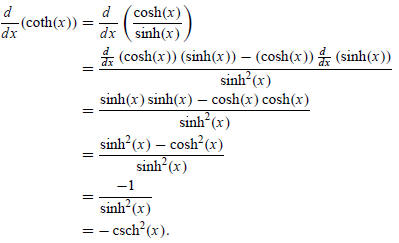
The remaining two hyperbolic trigonometric functions are handled similarly:

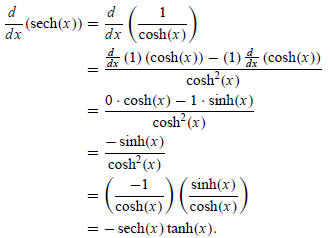
and

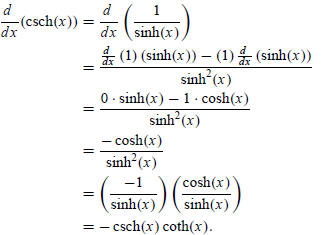
Inverse Hyperbolic Trigonometric Functions

The four functions



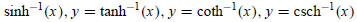
are one-to-one on their domains, while the functions



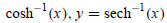
are one-to-one on the interval x ≥ 0. So, we can define six inverse hyperbolic trigonometric functions .

Since the hyperbolic functions are defined in terms of the exponential function, it is only natural to expect that
the inverse hyperbolic functions can be defined in terms of the natual logarithm function . We derive these six formulas
next: