How Do Scientists Deal with Very Large and Very Small Numbers
Introduction
To make calculations in science we must often deal with very big and very small
numbers. For
example, the distance between the Sun and the Earth is 150,000,000,000 m. It is
inconvenient to
have to write all those zeros all the time . Also, writing all those zeros
increases the chance of
errors by getting the number of zeros incorrect. Thus, scientists have developed
“scientific
notation” to better work with very large and small numbers. We will be using
scientific notation
throughout the course. This exercise will provide an introduction to or review
of scientific
notation.
What is scientific notation and how is it used?
Scientific notation is a “shorthand” way of writing very large and very small
numbers. Scientific
notation is based on powers of base number 10. The general format looks
something like this:
N X 10x
where N is a number greater than 1, but less than 10 and x
is an exponent of 10.
Placing numbers in exponential notation has several advantages.
1. For very large numbers and extremely small ones, these numbers can be placed
in
scientific notation in order to express them in a more concise, compact form.
2. In addition, numbers placed in this notation can be used in a computation
with far
greater ease.
Numbers Greater Than 10
Let’s first discuss how we will express a number greater
than 10 in such notational form.
1. We first want to locate the decimal and move it either right or left so that
there are
only one non-zero digit to its left.
2. The resulting placement of the decimal will produce the N part of the
standard
scientific notational expression.
3. Count the number of places that you had to move the decimal to satisfy step 1
above .
4. If it is to the left as it will be for numbers greater
than 10, that number of positions
will equal x in the general expression.
As an example, how do we place the number 23419 in standard scientific notation?
1. Position the decimal so that there is only one non-zero digit to its left. In
this case we
end up with 2.3419
2. Count the number of positions we had to move the decimal to the left and that
will be
x.
3. Multiply the results of step 1 and 2 above for the standard form: So we have:
2.3419
X 104
Numbers Less Than One
We generally follow the same steps except in order to position the decimal with
only one nonzero
decimal to its left, we will have to move it to the RIGHT. The number of
positions that we
had to move it to the right will be equal to -x. In other words we will end up
with a negative
exponent.
Negative exponents can be rewritten as values with positive exponents by taking
the inversion of
the number. For example: 10-5 can be rewritten as 1/ 105.
Here is an example to consider: Express the following number in scientific
notation: 0.000436
1. First, we will have to move the decimal to the right in order to satisfy the
condition of
having one non-zero digit to the left of the decimal. That will give us: 4.36.
2. Then we count the number of positions that we had to move it, which was 4.
That will
equal -x or x = -4. And the expression will be 4.36 X 10-4.
Numbers Between 1 and 10
For those numbers we do not need to move the decimal so the exponent will be
zero. For
example: 7.92 can be rewritten in notational form as: 7.92 X 100. Recall 100.is
equal to 1.
Exercises
Express the following numbers in their equivalent scientific notational form:
| Number | Scientific Notation |
| 123,876.3 | |
| 1,236,840. | |
| 4.22 | |
| 0.000000000000211 | |
| 0.000238 | |
| 9.10 |
One of the advantages of this notation that was mentioned
earlier in the exercise was the ability
to compute with them in an easier fashion than with actual numerical
equivalents .
Multiplication of Numbers Using Scientific Notation
The general format for multiplying using scientific notation is as follows: (N X
10x) (M X 10y) =
(N) (M) X 10x+y.
1. First multiply the N and M numbers together and express an answer.
2. Secondly multiply the exponential parts together by ADDING the exponents
together.
3. Finally multiply the two results for your final answer.
For example: (3 X 104) (1 X 102)
1. First 3 X 1 = 3
2. Second (104) (102) = 104+2 = 106.
3. Finally 3 X 106 for the answer.
Another example: (4 X 103) (2 X 10-4)
1. First 4 X 2 = 8.
2. Secondly (103) (10-4) = 10 3+(-4) = 10
3-4 = 10-1.
3. Finally 8 X 10-1 would be the answer.
Exercises
Express the product of the following:
| Calculation | Answer in Scientific Notation |
| (3 X 105) (3 X 106) = | |
| (2 X 107) (3 X 10-9) = | |
| (4 X 10-6) (4 X 10-4) = |
Division of Numbers Using Scientific Notation
The general format is as follows:
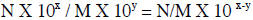
Before we get into some examples of this type of mathematical operation , lets
review the
conventional rules for combining signs that have been multiplied together. First
there are two
types of SIGNS in math . There are operational signs that indicate a specific
math operation to be
performed. A plus sign might indicate summation where a negative sign might
indicate a
subtraction. Then there are value signs that ascribe a certain value to a number
such as a -5
contrasted with a +5 in value. One would have a value that is five units to the
left of the zero
position on a number line and the other would have a value of five positions to
the right of the
zero position of a number line.
According to a set of conventional rules if an operational sign is multiplied by
a value sign and
both are in the same mode (both plus or both minus) then they are replaced by a
single sign that
is positive. So for example: -(-) = + or +(+) = +
On the other hand if the operational and value signs are of opposite mode (one
plus while the
other is negative) then the rule states that the two signs are replaced by a
negative sign. So for
example: -(+) = - or +(-) = -
Keeping these sign rules in mind let us approach division with an example. 6 X
105 / 2 X 102 =
1. Perform the division on the N and M numbers, 6 / 2 = 3
2. Perform the division on the exponential parts by subtracting the exponent in
the lower
number from the exponent in the upper number.
So 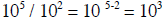
3. Multiply the two results together, 3 x 103
Let’s take another example, 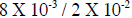
1. First 8 / 2 = 4
2. Subtracting (operational sign is negative) a -2 (where the value sign is also
negative)
from a -3. According to the sign rules the operational sign that is negative and
the
value sign which is also of the SAME mode (negative) will be replaced by a
positive
sign so -(-2) = +2.
3. So: 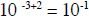
4. Multiply the result of step 1 above with the result of
step 3 above to get the answer: 4
X 10-1
Exercises
Express the quotients of the following:
| Calculation | Answer in Scientific Notation |
| 3.45 X 108 / 6.74 X 10-2 = | |
| 6.7 X 107 / 8.6 X 103 = | |
| 4.7 X 10-2 / 5.7 X 10-6 = |
Addition and Subtraction Using Exponential Notation
We can discuss these together since the important thing to remember about adding
or subtracting
is that the exponents must be the same before the math operation can be
performed. The general
format would be:  or
or
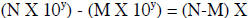
10y
If the exponential equivalents do not have the same exponent then the decimal of
one has to be
repositioned so that it's exponent is the same as all the rest of the numbers
being added or
subtracted. The reason for that is that when we add or subtract numbers we must
line all the
decimals up in the same position before we add or subtract columns of numbers.
So for example:
(2.3 X 10-2) + (3.1 X 10-3)
We recognize that the two exponents are not the same so either the exponent of
the first number
has to be changed to a -3 or the exponent of the second number has to be changed
to a -2. It is
really arbitrary which one is changed. Let's change the first one. 2.3 X 10-2
Remember for each position to the right we add a -1 to the exponent and for each
position to the
left we add a +1 to the exponent. In this case we must reposition the decimal
one position to the
right so it becomes: 2.3 X 10-2 +(-1) = 23. X 10-3
Now both numbers will have the SAME exponent value.
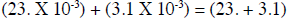
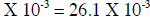
Here is another example: (4.2 X 104) - (2.7 X 102) = ? Lets adjust the exponent
of the second
number this time. Remember it is arbitrary which one we adjust. 2.7 X 102 must
be repositioned
two places to the left so that we will add a +2 to the exponent to make it the
same value as the
exponent of the first number. 2.7 X 102 becomes .027 X 102+2
= .027 X 104
Now the problem reads 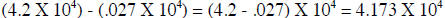
Exercises
Identify the sums or differences of the following:
| Calculation | Answer in Scientific Notation |
| (8.41 X 103) + (9.71 X 104) = | |
| (5.11 X 102) - (4.2 X 102) = | |
| (8.2 X 102) + (4.0 X 103) = | |
| (6.3 X 10-2) - (2.1 X 10-1) = |
| Prev | Next |