HINTS ON MATH 102 HOMEWORK 8
§.8.3.
Part 1
We understand that you may not have done algebra for a while , so you may face
some real difficulty when you are integrating rational functions . Below are a
few
examples of how you could deal with such integrals; in particular, focus on why
and how the rational functions are decomposed into partial fractions. They are
almost the same as the assigned homework problems, except that some numbers
are different. Hopefully that will give you a hint on how to solve the homework
problems.
(1)
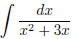
First one should see that such a fraction is a rational
function, meaning
that both the numerator (1 in this case) and the denominator (x2 + 3x
in this case) are polynomials. This suggests that techniques in handling
rational functions should be used. There are two main techniques: the
first one being an reduction (say by completing the square ) to one of those
formula in Section 8.1 (or Handout 3), which is applicable whenever the
denominator cannot be factorized, and the second one being decomposition
into partial fractions, which is applicable whenever the denominator can be
factorized. So let's do this integral.
First, the denominator of the integral is x2 + 3x. Can it be factorized?
In other words, can you write it as product of other ( lower -degree) polyno-
mials? (If you are unfamiliar with factorization, stop here and browse the
corresponding webpage that I have posted about factorization of polyno -
mials to remind yourself of how that works; we will just need some simple
factorizations for the moment.)
Yes, we have x2 + 3x = x(x + 3). So we would like to use the partial
fraction technique. In other words, we want to write
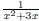as combinations
of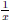 
and 
.
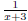So what do we do?
Let
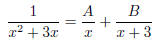
where A and B are constants (meaning that they are numbers
that does
not depend on x). We want to figure out what A and B are. Let's simplify
the right hand side and compare with the left -hand side. The right hand
side is
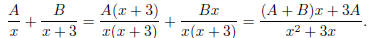
So to make it match with the left hand side, we need
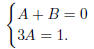
Solving, we get
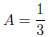and
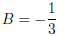
so
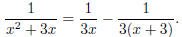
(This can also be checked directly if you just compute
what the right hand
side is.) From here we can calculate the given integral, because the right
hand side is easy to integrate:
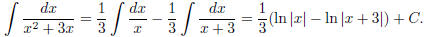
This completes the solution.
(2) Try now
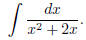
(3)
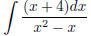
Again, this is a rational function. Let's check whether
the denominator can
be factorized:
Yes! x2 − x = x(x − 1). So we want to do partial fraction:
Let
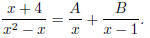
(Why?) Then the right hand side is
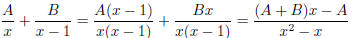
so comparing coefficients , we get
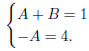
i.e. A = −4, B = 5. So
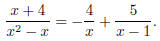
Integrating, we get
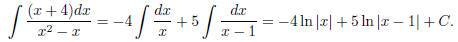
(4) Try now
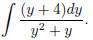
(5) So the success of the whole method relies on two
things: first that you can
factorize the denominator, and second that you can decompose the given
rational function into (simpler) partial fractions that you can handle. The
first bit could be hard if you haven't done it for a while. Here is a brief
review of what you should know:
• Factorizing out any common factors in x (e.g. x2 + 3x, x3 + x)
• Factorizing difference of squares (e.g. x2 − 4, x2 − 1, 4x2 − 9)
• Factorizing a general quadratic polynomial (e.g. x2 − 7x + 12, 4x2 −
4x + 1)
If you have no trouble factorizing any of these you should
basically be fine.
If you have difficulty with any of them, read the webpage about factorization
before you proceed.
(6) Now a slightly more difficult one:
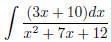
First, factorize the denominator: x2 + 7x + 12 = (x + 3)(x
+ 4).
Next, decompose the given fraction into partial fractions: Let
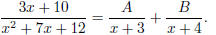
The right hand side is
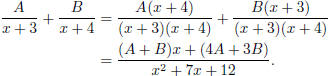
Comparing coefficients, we get
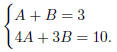
It's not hard to solve this pair of equations : in case you
have forgotten,
here is how to do it. By the first equation, A = 3−B, so we can substitute
this into the second one, and get
4(3 − B) + 3B = 10
(we can do this substitution because both equations are simultaneously
true). In any event, we get 12−B = 10, i.e. B = 2, so A = 3−B = 3−2 = 1,
or in other words the solution is A = 1 and B = 2. Hence now
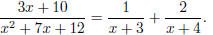
Integrating, we get
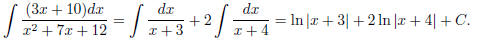
(7) Try now
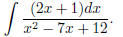
(8) If you have taken the pain to go through all the above
and reached here,
you probably deserve a break. Here is a joke:
Q: Why do you rarely find mathematicians spending time at the beach?
A: Because they have sine and cosine to get a tan and don't need the
sun!
Read on...
(9) Sometimes you have to factorize a little bit more:
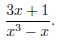
Let's factorize the denominator: x3−x = x(x2−1). But wait,
this is not
the end yet! Because x2−1 can be further factorized: x2−1 = (x−1)(x+1).
So altogether,
x3 − x = x(x − 1)(x + 1).
The game is that you will always have to factorize as
completely as possible
before you do partial fractions.
Now we do partial fractions: Let
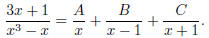
Then the right hand side is equal to
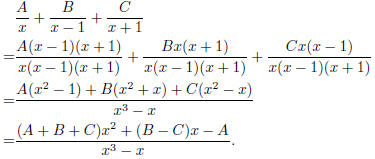
So we get
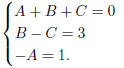
Hence A = −1, and
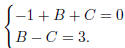
Solving, we get B = 2 and C = −1. So
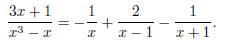
Integrating, we get
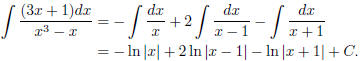
(10) Try now
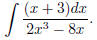
| Prev | Next |