Factoring

Factoring out a Common Factor: The first step in factoring any polynomial is to
look for anything that all the terms have in common and then factor it out using the
distributive property .
Example: 20y² - 5y⁵ Here, the terms share the common factor 5y² (i.e. 5 is the largest
number that divides both 20 and 5, and both terms contain the variable y with 2 being
the smallest exponent ). So we factor it out: 20y² - 5y⁵ = 5y²(4 - y³)

Factoring by Grouping: Factoring by grouping is useful when we encounter a polynomial
with more than 3 terms.
Example: 3x³ + x² - 18x - 6

1. First, we group together terms that share a common factor . (3x³ + x²) + (-18x - 6)
The first group shares an x² and the second shares a -6.

2. Factor out the common factor from each grouping. You should have left the same
expression in each group . x²(3x+1)+(-6)(3x+1) Here that expression is 3x+1

3. Now factor out that expression. (3x + 1)(x² - 6)

  Factoring Trinomials - Reverse FOIL: There two basic cases that we’ll encounter:

1. The leading coefficient is a 1. This is the easier of the two cases: x² + bx + c All
we need to do here is find two numbers whose product is c and sum is b
Example: x² - 7x + 10 = (x + △)(x + △) We need to find two numbers that
multiply to give us +10, but add to give us -7. Well, -5 and -2 do the trick. So
x² - 7x + 10 = (x + (-2))(x + (-5)) = (x - 2)(x - 5)

2. The leading coefficient is not a 1. Things are a little trickier here, but not much.
Again, it’s just FOIL in reverse.
Example: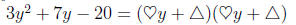
We need two numbers to fill in for the hearts that will multiply to 3. How about
3 and 1?
3y² + 7y - 20 = (3y +△)(1y + △)
Now we need two numbers to fill in for the triangles that will multiply to -20
AND when we do the INNERS and OUTERS we get 7y. We’ll use the GUESS
and CHECK method to find the two numbers we need.
Let’s try 10 and -2 first:
(3y - 2)(y + 10) = 3y² + 30y - 2y - 20 = 3y² + 27y - 20
That’s not it! Maybe 5 and -4?
(3y + 5)(y - 4) = 3y² - 12y + 5y - 20 = 3y² - 7y - 20
Close, but the sign on the 7 is wrong . Easy to fix - just switch the signs on the 5
and 4:
(3y - 5)(y + 4) = 3y² + 12y - 5y - 20 = 3y² + 7y - 20 Presto!!

Special Factorizations: Some polynomials are easy to factor because they fit a
certain mold.

– Difference of Squares : F² - L² = (F + L)(F - L)
Example: 16x² - 9 = 42x² - 3² = (4x)² - 3² = (4x + 3)(4x - 3)

– Perfect Squares : These are polynomials that factor into (F + L)² or (F - L)²
The pattern we’re looking for here is F² + 2LF + L² or F² - 2LF + L²
Example: x² + 6x + 9 = x² + 2·3x + 3² = (x + 3)²
Example: y² - 10y + 25 = y² - 2·5y + 5²

– Difference of Cubes : F³ - L³ = (F - L)(F² + LF + L²)
Example: 2z³ - 54 = 2(z³ - 27) = 2(z³ - 3³) = 2(z - 3)(z² + 3z + 9)

– Sum of Cubes: F³ + L³ = (F + L)(F² - LF + L²)
Example: n³ + 216 = n³ + 6³ = (n + 6)(n² - 6n + 36)

 Strategy for Factoring:

1. Always factor out the largest common factor first. This will make life easier for
any further factoring that may need to be done.

2. Look at the number of terms
– Two terms: Is it a difference of squares, difference of cubes or sum of cubes?
– Three terms: Is it a perfect square? Try reverse FOIL.
– Four or more terms: Try factoring by grouping.

3. Always make sure the polynomial is factored COMPLETELY.