Differential equations Problem Set 6
Please answer all of the following questions. The problems marked with an
asterisk will be
graded while the remained problems will be checked for completeness. Staple your
work to
this sheet of paper and indicate your answers clearly. Don’t forget your name
and please
circle your section number.
1. Section 10.1 (pp. 575–576) 5, 6, 7, 9, 15*, 16*.
2. Section 10.2 (pp. 585–587) 14*, 15, 17.
3. A second- order Cauchy -Euler equation has the form
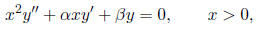
where α are β are
constants (see Section 5.5). Homogeneous solutions of this equation may
be found in a similar manner as those for constant coefficient equations . The
purpose of
this exercise is to illustrate this point.
(a) Show that y = xr is a solution of the Cauchy-Euler equation if r
satisfies the characteristic
polynomial
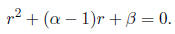
Let us now assume that r1 and r2 are roots of the characteristic polynomial
obtained using
the quadratic formula . There are three cases to consider.
1. If r1 and r2 are real and unequal, then the general solution has the form
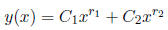
2. If r1 and r2 are complex
conjugates, equal to λ±iμ say, then the general solution has
the form
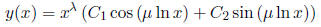
3. If r1 = r2 = r, then the general solution has the form
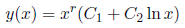
(b) Find general solutions for the following equations .

Parts (a) and (b) are “starred” problems.
| Prev | Next |