Brief Review of Linear and Quadratic Functions
Do all of these without using your calculator. You may use
your calculator to check your
work.
1. Solve the equations for x .
a. 2-3(5-2x)+7x = 3x +8
b.
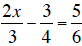
c. 3x2 - 7x = 6 (Solve by factoring.)
d. 2x2 +1= -5x
2. Find the equation of the line that passes through the point (-3, 5) and has
slope of
-2/3. Write the equation in slope- intercept form . Graph this line.
3. Find the slope of the line through the points (-325, 126) and (-416, -519).
4. Graph the function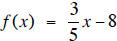 
. What is the x-intercept?
5. If x-y data is graphed with x representing the number of acres and y
representing
the number of cows, what are the units on the slope of the line between two of
the
data points?
6. Find the x- and y-intercepts and complete the square to find the vertex .
Graph the
function
f (x) = 2x2 + 5x -12.
7. Let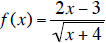 
.
a. Find the domain of f.
b. Find f(5).
c. Find f(x-2).
d. How does the graph of f(x-2) differ from the graph of f(x)?
e. How does the graph of f(x)-2 differ from the graph of f(x)?
f. How does the graph of 0.2f(x) differ from the graph of f(x)?
Partial Solutions and Answers .
1.Solve the equations for x.
a. 13x-13=3x+8 so x = 21/10 or 2.1.
b. 8x-9=10 and so x=19/8 or 2.375.
c. (x-3)(3x+2)=0 and so x=3, x= -2/3 are solutions .
d. Using the quadratic formula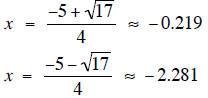 
2.
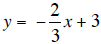is the slope-intercept form. Check your graph on the
calculator..
3.
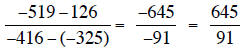
4. The x-intercept is 40/3. Check the graph on your calculator.
5. 
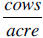. Units on slope are the vertical axis units divided by the horizontal
axis units.
6. y-intercept (Set x=0): y=-12
x-intercepts (Set y=0 and solve the quadratic equation ): x = 3/2 and x= -4.
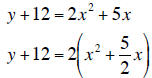
Vertex :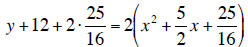 
note :
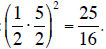
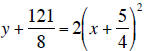
vertex :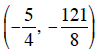 
7. Let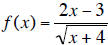 
.
a. Find the domain of f. Cannot take square roots of negative numbers so x+4 is
greater than 0. Cannot divide by 0 so x+4 does not equal 0. Answer: x> -4.
b.
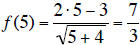
c.
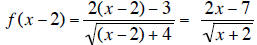
d. Shift f(x) 2 units to the right.
e. Shift f(x) 2 units down.
f. Graph is vertically shrunk by a factor of 0.2.
| Prev | Next |