Solutions to Math Homework 4

Ch 3.2 no. 1.
(a) A point A is said to lie between points A and B, denoted A − C − B, if
A,B,C are distinct and d(A,B) = d(A,C) + d(C,B).
(b) For two distinct points A,B a line segment 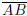consists of the points A,B
and of all points C on the unique line passing through A and B such that A−C−B.
The points A and B are called the endpoints of .
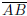(c) If A,B,C are three distinct non-colinear points, then the angle∠BAC consists
of the points on rays 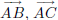and of all points D that lie between a point on
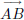and a point on 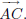The rays 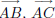are called the sides of ∠BAC and the
point A is called the vertex of ∠BAC.
(d) An angle is obtuse if it has measure more than 90° . An angle is acute if it
has measure less than 90° . An angle is right if it has measure 90° .
(e) Two angles are adjacent of they have a common side and their intersection
is equal to that side.
(f) Two angles are vertical if they have a common vertex , their intersection is
equal to that vertex and if the sides of each angle can be ordered in such a way
that the union of the first sides of these angles is a line and the union of the second
sides of these angles is a line.
(g) Two angles are supplementary if the sum of their measures is 180° . Two
angles are complementary if the sum of their measures is 90° .
(h) The midpoint of a line segment is a point on the segment that is equidistant
from the endpoints of the segment.
(i) A bisector of an angle ∠BAC is a ray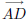 that is contained in ∠BAC and
such that m∠BAD = m∠DAC = 1/2m∠BAC.
(j) Two lines l ₁, l₂ are said to be perpendicular if they intersect at a point A such
that for any point B on l₁ and any point C on l₂ such that B ≠ A and C ≠ A the
angle ∠BAC is right.
(k) If A,B,C are three non-colinear points then a triangle Δ ABC is the intersection
of the angles ∠ABC, ∠BAC and ∠CBA. The points A,B,C are called
vertices of ΔABC and the segments 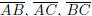are called the sides of ΔABC.
(l) Let A₁,A₂,A₃, . . .A_n (where n ≥ 4) be n distinct points in the plane.
Suppose that:
(1) No three distinct points in the list A₁,A₂,A₃, . . .A_n are colinear; and
(2) For each i = 2, . . . , n − 2 the intersection of the triangles ΔA₁A_iA_i+1 and
A₁A_i+1A_i+2 is equal to the segment 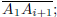and
(3) The union of the triangles ΔA₁A₂A₃,ΔA₁A₃A₄, . . .Δ,A₁A_n-1A_n is convex.
Then a polygon P(A₁, . . . ,A_n) is the union of triangles
ΔA₁A₂A₃,ΔA₁A₃A₄, . . . ,ΔA₁A_n-1A_n.
The points A₁, . . . ,A_n are called the vertices of P(A₁, . . . ,A_n) and the segments
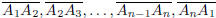are called the sides of P(A₁, . . . ,A_n).
(m) The interior of an angle (triangle, polygon) consists of all those points of
the angle (triangle, polygon) that do not lie on its sides.

Ch 3.2 no. 4
We will show that the relation of angle congruence is an equivalence relation.
Recall that the angles 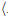ABC and ∠A′B′C′ are said to be congruent, denoted
ABC 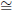∠A′B′C′, if m∠ABC = m∠A′B′C′.
(1) Reflexivity. For any angle ∠ABC we have m∠ABC = m∠ABC and hence
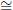∠ABC ∠ABC.
(2) Symmetry. Suppose ∠ABC 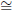∠A′B′C′.
Then m∠ABC = m∠A′B′C′. Therefore m∠A′B′C′ = m∠ABC and hence
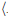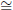A'B'C' ∠ABC.
(3)Transitivity. Suppose 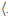ABC 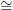∠A'B'C' and 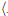A'B'C' 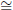∠A"B"C"
Then m∠ABC = m∠A′B′C′ and m∠A′B′C′ = m∠A"B"C". Hence m∠ABC =
m∠A"B"C" and so 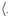ABC 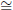∠A"B"C"

Ch 3.2 no. 6.
We need to prove that supplements and complements of congruent angles are
congruent. We will do that for complements.

Suppose α, β , are angles such that 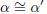and let β be a complementary angle of
α and β' be a complementary angle of α'. We need to show that

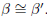
Since 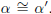we have mα = mα' . Since β is a complement of α and β' is a
complement of α', we have mβ = 90° − mα and mβ'  = 90° − mα' . Hence

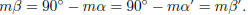
Thus 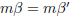and 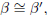as required.

Ch 3.2 no. 7. (Draw a picture for the argument below)
We need to prove that vertical angles are congruent.

Suppose angles ∠BAC and ∠B'AC' are vertical, so that 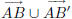is a line l₁
and 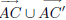is a line l₂.

Since the angles ∠BAC and CAB' form a linear pair , SMSG Postulate 14 implies
that these angles are supplementary and so m∠BAC + m∠CAB' = 180° .

Similarly, the angles ∠CAB' and B'AC' form a linear pair and therefore by
SMSG Postulate 14 these angles are supplementary and m∠CAB' + m∠B'AC' =
180° .

Therefore
m∠C'AB' = 180° − m∠CAB' = 180° − (180° − m∠BAC) = m∠BAC
Thus m∠C'AB' = m∠BAC and so ∠C'AB' 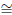∠BAC, as required.

Ch 3.2 no. 9. (Draw a picture for the argument below)
We need to prove that if a point is on a perpendicular bisector of a line segment,
then it is equidistant from the endpoints of that segment.

Let l be a perpendicular bisector to a segment 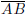and denote the midpoint of
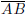by T.

Suppose C is a point on l.

If C = T then d(C,A) = d(C,B) = 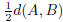and C is equidistant from A and
B. Suppose now that C ≠ T, so that A,B,C are not co- linear .

We have ∠CTA 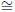∠CTB, since both angles are right. Moreover, 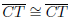and
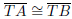since d(A, T) = d(B, T).

Therefore by the SAS axiom (SMSG Postulate 15) ΔCTA 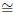ΔCTB. This
implies that 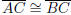and so d(A,C) = d(B,C), as required.