Math 544, Exam 1 Information
Exam1 will be based on:
• Sections1.1 - 1.3,1.5 - 1.7,and 1.9.
• The corresponding assigned homework problems
At minimum,
you
need to understand how to do the homework problems.
• Lecture notes: 1/17- 2/12.
Topic List(not necessarily comprehensive):
You will need to know how to define vocabulary words/phrases defined in class.
§1.1: Matrix representation of a linear system: coefficient matrix, augmented
matrix, ele-
mentary row operations ,row equivalence.
§1.2: Solving linear systems via Gauss- Jordan elimination : echelon and reduced
echelon
forms of a matrix, identifying dependent and independent variables , recoginizing
when a
system is consistent /inconsistent.
§1.3: Relationship between # nonzero rows and # columns in an augmented matrix
in re-
duced echelon form. Homogeneous linear systems . # possible solutions to
1. a general linear system .
2. an m×n system with m < n.
3. a homogeneous system .
§1.5: Matrix operations: addition, multiplication, multiplication by scalars,
scalar (dot)
product in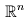 
.
§1.6: Properties of matrix addition,multiplication,and multiplication by scalars.
The matrix
transpose and its properties ,scalar (dot) product and its relation to
vector norm (length).
§1.7: Linear combinations, linear dependence/independence: determinination of
whether a
given set of vectors is linearly dependent /independent. Non-singular matrices;
conditions
equivalent to non -singularity of A ∈ Matn×n:
1. Ax=θ has only the trivial solution x =θ
2. columns of A are linearly independent
3. 
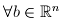, Ax b has a unique solution .
4. A is invertible.
5. A is row equivalent to the identity ,In.
§1.9: Matrix inverses: existence of inverses (see above,e.g.,A is invertible
A is non-
singular),using inverses to solve systems ,computing inverses by row reduction ,formula for
inverse of 2 ×2; matrix, algebraic properties .
| Prev | Next |