Math 236 Chapter Outline
Be sure to read the Disclaimer on Chapter Outlines! I
cannot be responsible for misfortunes
that may happen to you if you do not.
7.1 One-to-One Functions; Inverses
•
Definition and properties of one -to-one functions: Algebraic definition of
one-to-
one and its contrapositive. Graphical interpretation of one-to-one. Functions
that
are always increasing or always decreasing are one-to-one (why?). Be able to use
all
three of these methods to determine if a function is one-to-one.
• Definition, properties, and graphs of inverse functions: Algebraic
definition of
inverse function. Graphical relationship between a function and its inverse. A
function
has an inverse if and only if it is one-to-one. Properties of one-to-one
functions (for
example, (a, b) is on the graph of f (x) if and only if (b, a) is on the graph
of f' (x)).
Domains and ranges of inverse functions. Be able to calculate the inverse of a
one-to-one
function algebraically, and graph the inverse of a function given the graph of
the
original function.
• Derivatives of inverse functions: Know and be able to prove and explain
the
formula for the derivative of an inverse function. Be able to use this formula
to
calculate the derivative of the inverse of a function at a given point (even if
you are
unable to find an equation for the inverse function).
7.2 The Logarithm Function , Part I
• Definition and properties of general logarithm functions: Definition of a
logarithm
function in general. Know and be able to prove the properties that follow
from the definition of a logarithm function. Understand the steps of the proof
that
the derivative of a logarithm function is always a constant times
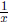 .
.
•
Definition properties, and graph of ln x: Be able to explain how we chose a
"natural" logarithm function by setting f'(1) = 1. Know the definition of the
natural
logarithm function (as a definite integral), and know how we got that definite
integral.
Be able to approximate values of ln x using this definition (and a Riemman sum ).
Algebraic and graphical properties of ln x, domain and range of ln x, and
arguments
why these things are true. Definition of the number e and its relationship to ln
x.
Solve equations involving ln x.
• The derivative of ln x: Use the definition of ln x and the "Very
Important Theorem"
to find the derivative of ln x. Be able to differentiate complicated functions
that involve
ln x.
7.3 The Logarithm Function, Part II
• The derivative of 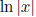 : Split
: Split
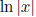 into a piecewise function to see that its
derivative
into a piecewise function to see that its
derivative
is ![]() .Know the graph of
.Know the graph of
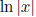 and why we were interested in finding its
derivative
and why we were interested in finding its
derivative
(rather than just the derivative of ln x). Note that this derivative formula
does not
tell us what the integral of ln x or 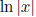 should
be.
should
be.
• The integral of ![]() : Knowing the above tells us how to antidifferentiate
: Knowing the above tells us how to antidifferentiate
![]() . Understand
. Understand
the difference between the fact that the antiderivative of
![]() is
is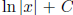
and the fact that the definition of ln x involves a definite integral of
![]() . Be able to
. Be able to
do integrals that involve
![]() and
and
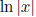 , including u-substitution problems. As with
, including u-substitution problems. As with
all sections having to do integration, know how to do associated volume and
position/
velocity/acceleration problems.
•
Integrating the trigonometric functions : The information above can be used
to
integrate the four trig functions whose integrals we did not already know. You
do not
need to memorize the integrals of tan x, cot x, sec x, and csc x, but you must
know
how to calculate them using u-substitution and the integral of
![]() .
.
• Graphing review: Be able to sketch the graph of a function (involving ln
x in
particular) by examining its first and second derivatives and its behavior at
the "ends"
of its domain. This includes identifying intervals of increasing/decreasing and
concave
up/down as well as finding local and global extrema, inflection points, points
of non-
differentiability, and asymptotes.
• Logarithmic differentiation: Know the formula for differentiating a long
product,
and be able to prove this formula using logarithmic differentiation. Be able to
apply
this formula to differentiate long products (or product/quotient combinations).
7.4 The Exponential Function
• The definition of ex, even for irrational x: Given any
x, know the definition of ex
as the unique number whose natural logarithm is x. Why did we need this
definition
(for irrational numbers x in particular)? Why does this definition imply that ex
is the
inverse of ln x?
• Properties and graph of ex: Be able to prove the functional and algebraic
properties
of ex using the definition of ex and the fact that ex and ln x are inverses.
•
The derivative of ex: Prove that the derivative of ex is ex directly (using
implicit
differenitation) and by using the formula for the derivative of an inverse
function. Be
able to differenitate complicated functions that involve ex, and use this
information
to sketch graphs of such functions. Know how to solve certain limits by
recognizing
them as derivatives of exponential functions.
• The integral of ex: The above information tells us the integral of ex.
Know this
and be able to use it in various integration problems, including applications.
7.5 Arbitrary Bases; Other Powers
• Definition and properties of xr, even for irrational r: Know the
definition of xr
involving the exponential and logarithmic functions. Why did we need this
definition
(in particular for irrational x)? Prove properties of xr using this definition
and known
properties of logarithmic and exponential functions.
• The derivative and the integral of xr: Prove the power rule by using the
definition
of xr above. Be able to use this rule. Know and be able to justify the integral
formula
for xr, and be able to integrate functions involving xr.
•
Definition, properties, and graphs of general exponential functions bx: Know
definition of bx (in terms of ex and logarithms, as we did for xr). Know how
graphs
of bx compare to each other and in particular to the graph of ex. Why do we
assume
b > 0 and b ≠ 1? Algebraic properties of bx are proved the same way we proved
those
for xr. Be able to convert from bx to ekx and vice-versa.
• The derivative and the integral of bx: Know and be able to prove the
"exponential
rule" derivative formula for bx (using the definition of bx). Do not confuse this
with
the formula for when the exponent is in the base. Know and justify the formula
for the
integral of bx. Be able to use the derivative and integral of bx in various
calculations.
• Derivatives of functions with variables in the base and exponent: Use
logarithmic
differentiation (take ln of both sides and apply implicit differentiation) to find
the derivatives of functions with a variable in the exponent and the base. Do
not try
to apply the power rule or exponential rule to these functions.
• Definition, properties, and graphs of general logarithmic functions
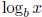 :
:
Definition of 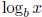 in terms of ln x and ln b. Know and prove properties of
in terms of ln x and ln b. Know and prove properties of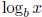
using the definition and properties of ln x. Be able to calculate certain values
of 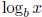
exactly by hand using these properties.
• The derivative of 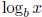 : Know and be able to prove the formula for the
derivative
: Know and be able to prove the formula for the
derivative
of 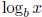 . Be able to use this both in differentiation problems and integration
problems
. Be able to use this both in differentiation problems and integration
problems
with u-substitution. Note that we do not know the integral of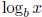 .
.
7.6 Exponential Growth and Decay
• "The rate of change is proportional to the quantity": Know and be able
to prove that f'(x) = kf (x) if and only if f (x) is an exponential function f (x)
=
Cekx. One direction is easy (just differentiate any exponential functions). The
other
direction involves solving the equation f' (x)- k f (x) = 0. Be able to do this
given the
hint that you will need to multiply both sides of the equation by e-kx.
• Doubling time and half-life: A function is exponential if and only if it
has a
constant doubling time or half life. Be able to explain what I mean by
"constant"
here. Be able to find doubling time or half-life given a particular exponential
functions.
Show that doubling time and half-life depend only on the continuous growth
constant
k.
• Yearly percentage growth and the continuous growth
constant: Know the
difference between the yearly percentage growth rate and the continuous growth
rate.
The first involves the b in Cbx, and the second is equal to the k in Cekx. Know in
a
word problem which of these is being discussed.
• Solving word problems involving exponential growth and decay: Be able to
identify problems where the rate of growth is proportional to the quantity, or
where
the function has a constant doubling time or half-life. In these problems the
quantity
is always an exponential function. Be able to find this function (by finding k and
C)
and find past or future values, doubling time or half-life of the quantity. This
includes
in particular population growth, radioactive decay, and (continuously)
compounded
interest.
7.7 The Inverse Trigonometric Functions
• Domains and ranges of the six inverse trigonometric functions: Know how
(and why) we restrict the domains of the six trigonometric functions so we can
obtain
inverses. Define the six inverse trigonometric functions as the inverses of these
restricted
domain functions. Know domains and ranges of all six inverse trig functions.
Be sure you understand the difference between the notation sin-1 x and sin2 x.
• Properties and graphs of the six inverse trigonometric functions:
Properties
of the inverse trig functions follow from their definition as the inverses of the
(restricted)
trig functions. Be able to use these and know when they apply and when
they do not. Be able to sketch the graphs of these inverse trig functions by
flipping
the graphs of the restricted trig functions over the y = x line .
•
Calculating exact values of trig and inverse trig functions: Use the unit
circle
to calculate exact values of the trig functions and the inverse trig functions
for values
that involve angles or side lengths (respectively) of the
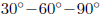 or 4
or 4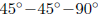 .
.
Obviously you need to memorize the side lengths of these triangles to do this.
Keep in
mind the domains and ranges when calculating values of inverse trig functions.
Know
how to convert degrees into radians and vice-versa.
• Derivatives of the six inverse trigonometric functions: Use implicit differentiation
to find the derivatives of the inverse trig functions. Use triangles to rewrite
these
derivatives in an algebraic form. Memorize the algebraic forms of these
derivatives
and be able to use them.
• Integrals involving inverse trig functions and their derivatives: Be able
to
do integrals involving u-substitutions with inverse trig functions and integrals
that
you can recognize as the derivatives of inverse trig functions. Be able to
convert an
integrand like, for example, 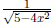 by algebra and
u-substitution into an integrand
by algebra and
u-substitution into an integrand
that is the derivative of an inverse trig function.
7.8 The Hyperbolic Sine and Cosine
• Definitions of hyperbolic sine and cosine: Know the definitions and be
able to
pronounce the names of sinh x and cosh x.
•
Derivatives of hyperbolic sine and cosine: Know and be able to prove the
derivative formulae for sinh x and cosh x. How does the derivative relationship
between
sinh x and cosh x motivate their names? (In other words, why give these
functions
these trig-sounding names when they involve ex?) Differentiate functions
involving
hyperbolic sine and cosine using either their definitions or their derivative
formulae.
• Properties and graphs of hyperbolic sine and cosine: Graph sinh x and
cosh x
using their derivatives and properties. How do their graphs compare to the graph
of
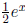 and why?
and why?
• Applications, Identities, and Hyperbolae: Be able to do word problems and
prove identities involving sinh x and cosh x. Know how sinh x and cosh x are
related
to a hyperbola (just as sin x and cos x are related to a circle ).
• Integrals involving hyperbolic sine and cosine: Use the definitions or
properties
or derivatives of sinh x and cosh x to solve integrals involving sinh x and cosh
x.
Sometimes it is best to use the definition to convert the hyperbolic sine and/or
cosine
into an expression into e x's, and sometimes it is best to use the derivatives of sinh x
and cosh x.
7.9 Other Hyperbolic Functions
• Definitions and properties of the remaining four hyperbolic trig functions:
Define the remaining four hyperbolic trig functions in terms of sinh x and cosh
x.
Be able to write these four functions in terms of ex's using these definitions.
Prove
identities involving these functions using these definitions.
• Derivatives of the remaining four hyperbolic trig functions: Find the
derivatives
of these four functions using their definitions and the derivatives of sinh x and
cosh x, or by using their definitions in terms of ex's. Sketch graphs of these
functions
using this derivative information.
• Integrals involving hyperbolic trig functions: As with sinh x and cosh x,
be able
to solve integrals involving the other four hyperbolic trig functions.
• Inverse hyperbolic trig functions: Find formulas for the inverses of the
six hyperbolic
trig functions by using their definitions in terms of ex's.
• Derivatives of inverse hyperbolic trig functions: Use these expressions
for the
inverse hyperbolic trig functions to calculate their derivatives. See in
particular exercises
19, 20, and 21 in 7.9. Memorize and be able to use these derivatives.
• Integrals involving inverse hyperbolic trig functions and their derivatives:
Use the derivatives of the inverse hyperbolic trig functions to solve integrals,
either by
u-substitution or by recognizing an integrand as the derivative of one of the
inverse
hyperbolic trig functions.
| Prev | Next |