Math 139A Midterm Exam

1. On your computer, select Internet Explorer, and find the website:

From here, enter your last name and student ID to log into the Math Placement test
system . Take test categories 6) Functions, and 7) Trigonometry. You don't need to
turn in anything for this question: I can access your scores directly.

2. Determine the formula for each of the two functions below:
(a) The function, V (t), representing the value of a home , which was purchased in
1980 (call this "t = 0") for $80; 000. The value of the home triples every 25 years.

(b) The quadratic function , f(x), containing points (-2;-18), (0; 0), and (3;-3)

3. Let .
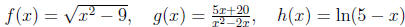(a) The domain of f(x): Dom(f) =

(b) The domain of g(x): Dom(g) =

(d) g(f(5)) =:

4. Let f(x) = cos(x³), and g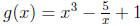. For each, state whether the function is:
i) even, ii) odd, or iii) neither.

5. Without a calculator or computer , sketch the approximate graphs of the functions:
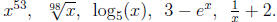. Indicate which graph below corresponds to which
function. (There's one extra grid if you screw up!)

6. Compute the inverse of the following functions:
(a)

(b)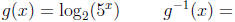

7. Simplify each of the following to determine it's value:

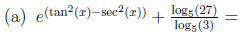
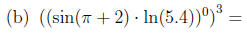
8. Prove any 2 of the following statements:
(a) Let f(x) be a function with domain 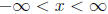. Then the function h(x) given
by: 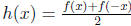is even, whether f(x) is even, odd, or neither.

(b) If a function f(x) is not one-to-one, then it has no inverse function.

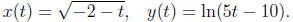
(d) sinh(x) + cosh(x) = e^x. (Hint: recall the de nitions of sinh and cosh.)

9. Use Maple for the following problem:
(a) Draw the function f(x) = sin(2x). Include gridlines, and pick a color (your choice)
for the graph . The view should be: 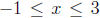and 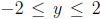. Print the
graph .

(b) On your graph, draw by hand the secant line which intersects your function at
x = 0 and x = 1. Compute the slope of this secant line.

(c) What is the average rate of change of f (x) over the interval 0≤x≤1? Explicitly
explain the relationship between this average rate of change and the secant line
your just drew.