Math 1 Practice for Final Exam
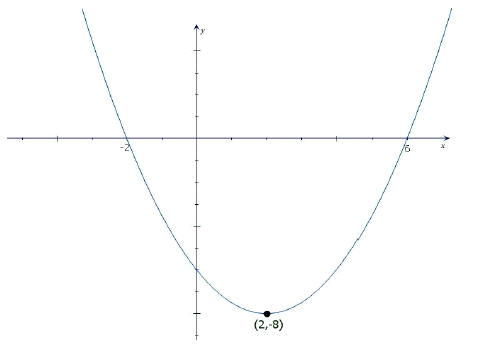
1. Find the quadratic function whose graph is shown here.
2. The freezing point of water is 0°C or 32°F. The boiling point is 100°C or 212°F.
(a) Express the Fahrenheit temperature F as a linear function of the
Celsius temperature C.
(b) If the temperature increases by 1°C, what is the corresponding increase in F temperature?
3. Find the domain of the function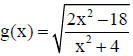 
. Write
your answer using interval notation.
4. An object launched directly upward at 64 feet per second (ft/s) from a
platform 80 feet high has a height of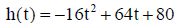 
where h
is measured in feet and t in seconds.
What will be the object's maximum height? When will it attain this height?
When will it hit the ground ?
5.
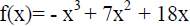Find all values of x such that f(x) > 0
and all x such that f(x) < 0.
Then use this information to sketch a graph of the polynomial f (x).
6. Find the domain and range of each function.
| Domain | Range | |
 |
||
 |
||
 |
||
 |
||
 |
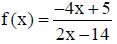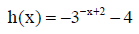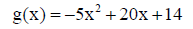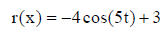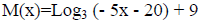7. Use the simple interest formula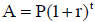 
to
find how long it will take your $3,000 investment to triple in value if you have
an interest rate of 8% ( r=.08) per year. Leave your answer in exact form, you
do not need to use a calculator .
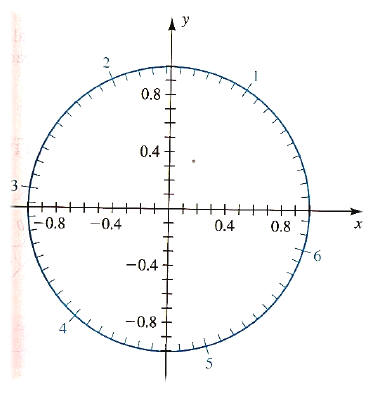
8. Use the figure at the right to approximate each value rounded to the nearest tenth.
• Sin 4
• Cos 2
• T, where sin T = .45 ( There are 2 answers for T )
• T, where cos T= -.65 (There are 2 answers for T)
9. Sketch one period of the function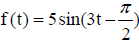 
.
Label the maximum and minimum values , also label the intercepts .
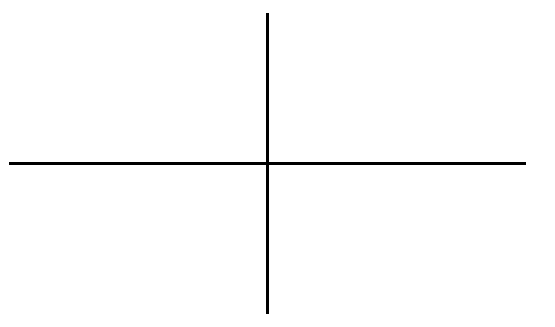
10. Use either an addition formula or a half angle formula to find, simplify your answers as much as you can.
(a) Cos(7π/8)
(b) sin(5π/12)
11. Given that tan(t)=2/5 and and sin(t) <0, find sin(2t) , find cos(2t) .
12. Given right triangle ABC, express sin(A) as a function of x.
Express cos(A) as a function of x .
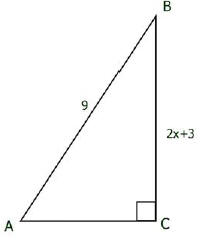
Using the answers you found above, verify the identity Cos2(A) + Sin2(A) = 1
13 . Which function has a greater average rate of change over the interval x=
- 1 to x=4,
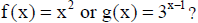Justify
your answer. This means explain your answer by showing your calculations .
Write your answer using a sentence.
14. The quadratic formula says that if a≠0, then the roots (solutions ) of
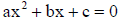are given by
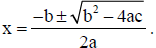Prove this formula by solving
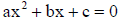by completing the square .
15. Graph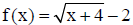 
and f-1(x) on the same coordinate system. Clearly label
the x and y intercepts for both your graphs.
What is f-1(x)?
State the domain and range for each function.
16. Let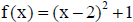 
Sketch a graph of f(x).
This function does not have an inverse function. Explain why.
How can you restrict the domain of f(x) so that you can
find an inverse function ?
Explain by drawing the graph of your new function. What is the domain of this
function?
What is the range ?
What is the domain of f-1(x)?
The range ?
Find f-1(x) for this function and graph it on the same coordinate system with f(x) .
17. Which of the following expressions , cos (1) or sin(1) , is larger ? Explain your reasoning using complete sentences and any drawing you might need to illustrate your explanation .
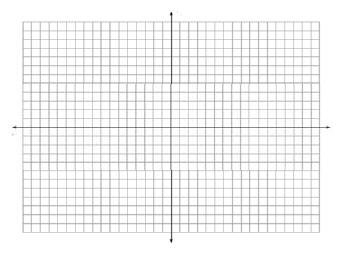
19. Solve each inequality and sketch the solution on a coordinate line. Also, write the solution in interval notation.
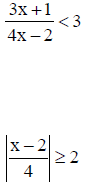
20. Solve for x in each equation .
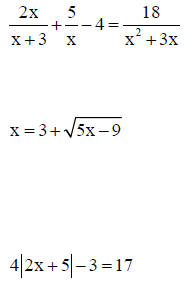
21. Graph the function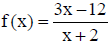 
.
Find all intercepts and asymptotes . What is the domain and range of f(x)?
Find f-1(x).
22. Find the quadratic function f(x) that satisfies :
• X intercepts are -3 and 5, maximum value is 4 .
• X intercepts are 8 and 0, minimum value is -48.
• Vertex is (1,2) and f(4)=8
23 An object is thrown vertically upward from the top of a
building. Its height in feet above the ground after t seconds is given by the
equation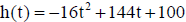 
.
• Find the maximum height above the ground.
• Find the height of the building .
| Prev | Next |