Learning Standards for Mathematics
| Mathematical Reasoning | Number and Numeration |
|
1. Students use mathematical reasoning to analyze mathematical situations, make conjectures, gather evidence, and construct an argument. Students: • construct simple logical arguments . • follow and judge the validity of logical arguments. • use symbolic logic in the construction of valid arguments. • construct proofs based on deductive reasoning. This is evident, for example, when students:  prove that an altitude of an
isosceles triangle, drawn to the prove that an altitude of an
isosceles triangle, drawn to thebase , is perpendicular to that base.  determine whether or not a
given logical sentence is a tautology. determine whether or not a
given logical sentence is a tautology. show that the triangle having
vertex coordinates of (0,6), (0,0), show that the triangle having
vertex coordinates of (0,6), (0,0),and (5,0) is a right triangle. |
2. Students use number sense and numeration to develop an understanding of the multiple uses of numbers in the real world , the use of numbers to communicate mathematically, and the use of numbers in the development of mathematical ideas. Students: • understand and use rational and irrational numbers. • recognize the order of the real numbers. • apply the properties of the real numbers to various subsets of numbers. This is evident, for example, when students:  determine from the
discriminate of a quadratic equation determine from the
discriminate of a quadratic equation whether the roots are rational or irrational.  give rational approximations
of irrational numbers to a specific give rational approximations
of irrational numbers to a specificdegree of accuracy.  determine for which value of x
the expression determine for which value of x
the expression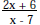 is undefined. is undefined. |
Sample Problems

| Key ideas are identified by numbers (1). Performance indicators are identified by bullets (•). Sample tasks are identified by triangles (  ). ). |
Students will understand mathematics and become
mathematically confident by
communicating and reasoning mathematically, by applying mathematics in
real-world settings, and by solving problems through the integrated study of
number systems, geometry, algebra, data analysis, probability, and trigonometry
| Operations |
Modeling/Multiple Representation |
|
3. Students use mathematical operations and relationships among them to understand mathematics. Students: • use addition, subtraction, multiplication, division, and exponentiation with real numbers and algebraic expressions. • develop an understanding of and use the composition of functions and transformations. • explore and use negative exponents on integers and algebraic expressions . • use field properties to justify mathematical procedures. • use transformations on figures and functions in the coordinate plane. This is evident, for example, when students:  determine the coordinates of triangle A(2,5), B(9,8), and C(3,6) determine the coordinates of triangle A(2,5), B(9,8), and C(3,6)after a translation (x,y) 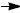 (x + 3, y - 1). (x + 3, y - 1). evaluate the binary operation defined as evaluate the binary operation defined asx * y = x2 + (y + x)2 for 3 * 4.  identify the field properties used in solving the equation identify the field properties used in solving the equation2(x - 5) + 3 = x + 7. |
4. Students use mathematical modeling/multiple representation to provide a means of presenting , interpreting, communicating, and connecting mathematical information and relationships. Students: • represent problem situations symbolically by using algebraic expressions, sequences, tree diagrams, geometric figures, and graphs. • manipulate symbolic representations to explore concepts at an abstract level. • choose appropriate representations to facilitate the solving of a problem. • use learning technologies to make and verify geometric conjectures . • justify the procedures for basic geometric constructions. • investigate transformations in the coordinate plane. • develop meaning for basic conic sections. • develop and apply the concept of basic loci to compound loci. • use graphing utilities to create and explore geometric and algebraic models. • model real-world problems with systems of equations and inequalities. This is evident, for example, when students:  determine the locus of points equidistant from two parallel lines. determine the locus of points equidistant from two parallel lines. explain why the basic construction of bisecting a line is valid . explain why the basic construction of bisecting a line is valid . describe the various conics produced when the equation describe the various conics produced when the equationax2 + by2 = c2 is graphed for various values of a, b, and c. |
Sample Problems
 |
|
|
Used with the permission of New Standards, copyright 1995. |
|
| Measurement | Uncertainty |
|
5. Students use measurement in both metric and English measure to provide a major link between the abstractions of mathematics and the real world in order to describe and compare objects and data. Students: • derive and apply formulas to find measures such as length, area, volume, weight, time, and angle in real-world contexts. • choose the appropriate tools for measurement. • use dimensional analysis techniques. • use statistical methods including measures of central tendency to describe and compare data. • use trigonometry as a method to measure indirectly. • apply proportions to scale drawings, computer-assisted design blueprints, and direct variation in order to compute indirect measurements. • relate absolute value, distance between two points, and the slope of a line to the coordinate plane. • understand error in measurement and its consequence on subsequent calculations. • use geometric relationships in relevant measurement problems involving geometric concepts. This is evident, for example, when students:  change mph to ft/sec. change mph to ft/sec. use the tangent ratio to determine the height of a tree. use the tangent ratio to determine the height of a tree. determine the distance between two points in the coordinate determine the distance between two points in the coordinateplane. |
6. Students use ideas of uncertainty to
illustrate that mathematics involves more than exactness when dealing with everyday situations. Students: • judge the reasonableness of results obtained from applications in algebra, geometry, trigonometry, probability, and statistics. • judge the reasonableness of a graph produced by a calculator or computer . • use experimental or theoretical probability to represent and solve problems involving uncertainty. • use the concept of random variable in computing probabilities. • determine probabilities using permutations and combinations. This is evident, for example, when students:  construct a tree diagram or sample space for a compound event. construct a tree diagram or sample space for a compound event. calculate the probability of winning the New York State Lottery. calculate the probability of winning the New York State Lottery. develop simulations for probability problems for which they do develop simulations for probability problems for which they donot have theoretical solutions. |
Sample Problems
 |
 Used with the permission of New Standards, copyright 1995. |
| Key ideas are identified by numbers (1). Performance indicators are identified by bullets (•). Sample tasks are identified by triangles (  ). ). |
Students will understand mathematics and become
mathematically confident by
communicating and reasoning mathematically, by applying mathematics in
real-world settings, and by solving problems through the integrated study of
number systems, geometry, algebra, data analysis, probability, and trigonometry.
Patterns/Functions
7. Students use patterns and functions to develop
mathematical power, appreciate the true beauty of
mathematics, and construct generalizations that
describe patterns simply and efficiently.
Students:
• use function vocabulary and notation.
• represent and analyze functions using verbal
descriptions, tables, equations, and graphs.
• translate among the verbal descriptions, tables,
equations and graphic forms of functions.
• analyze the effect of parametric changes on the graphs of
functions.
• apply linear , exponential, and quadratic functions in the
solution of problems.
• apply and interpret transformations to functions.
• model real-world situations with the appropriate
function.
• apply axiomatic structure to algebra and geometry.
• use computers and graphing calculators to analyze
mathematical phenomena.
This is evident, for example, when students:
 determine, in more than one way, whether or not a specific
determine, in more than one way, whether or not a specific
relation is a function.
 explain the relationship between the roots of a quadratic
explain the relationship between the roots of a quadratic
equation and the intercepts of its corresponding graph.
 use transformations to determine the inverse of a function.
use transformations to determine the inverse of a function.
Sample Problem

Used with the permission of
New Standards, copyright 1995.
| Prev | Next |