Intermediate Algebra Project Review
Intermediate Algebra 2 : Project 1 (Review)
Questions 1 through 30 are each worth 1 point. Questions 31 through 40 are
each worth 2 points.
Evaluate the following.
1.
2.For x < 0,
3. For x = 3,y = -2.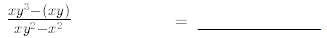
Simplify the following.
4.
5.
6.
Solve the following equations for all real values which make them true.
7.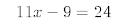
8.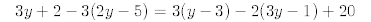
9.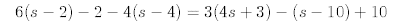
10.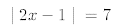
Rearrange the following formulas for the specified variable.
11.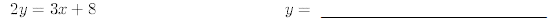
12.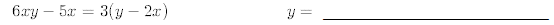
Solve and graph the solutions of the following inequalities.
13.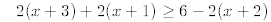
14.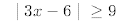
15.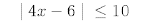
16. Which of the following relations define y as a function of x and which define x as a function of y ?

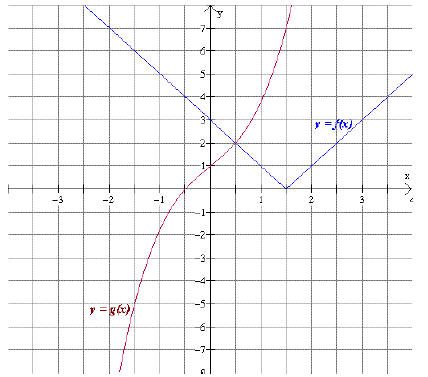
17. From the graphs of the functions, f(x)&g(x) , shown below estimate the following:
18. Graph the line 5x - 2y = 10
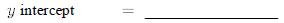
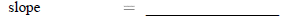
19.Graph the line 4x = 24
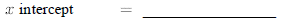
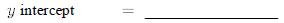
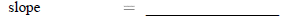
20.Find the equation (in slope- intercept form ) of the equation of the line which passes through (-2,7) and (1,1).
21.Giren f(x) = 3x2 - 2 and g(x) = x + 3,compute the following:
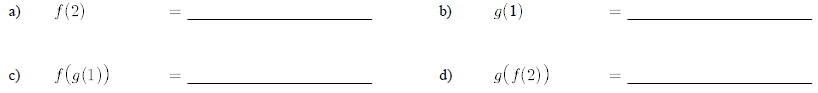
Perform the indicated operations and express the answer as a polynomial in
standard form.
22.
23.
24.
25.
26.
27. Perform the following polynomial long divisions.
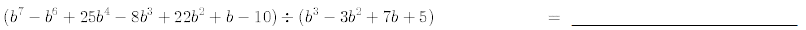
Use synthetic division to find the quotient and remainder of the following
divisions.
28.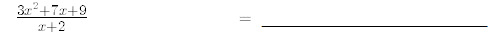
29.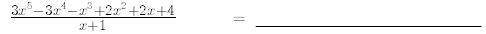
30. Given the polynomial,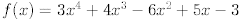 ,perform the
requested evaluations using synthetic division.
,perform the
requested evaluations using synthetic division.
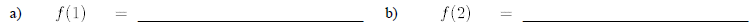
Factor the following polynomials as completely as possible:
31.
32.
33.
34.
35.
36.
37.
38.
Solve the following equations.
39.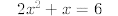
40.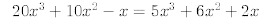
Intermediate Algebra 2 : Project 2 (Chapter 6)
Each problem is worth 2 points.
Simplify the following rational expressions :
1.
2.
3.
Perform the following operations and simplify the result:
4.
5.
6.
7.
8.
9.
10.
Express the following complex fraction as a simple rational expression in
reduced form.
11.
12.
13.Using WinPlot , generate and attach a computer plot of the following
function. Use the window :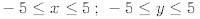
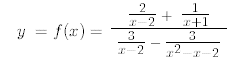
What value does C appear to have? Verify this by simplification.
Solve the following equations for all real solutions.
14.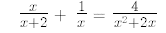
15.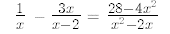
16.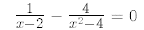
Solve the following literal equation for x .
17.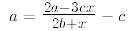
18.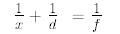
Solve and graph the following inequalities:
19.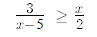
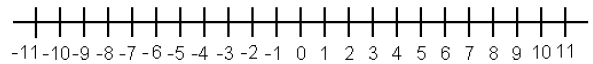
20.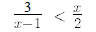
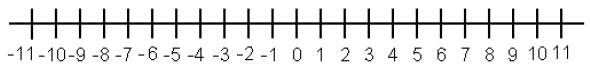
21.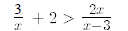
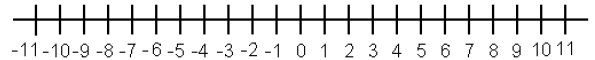
22.A storage tank has two inlet pipes. The smaller pipe takes minutes to fill
the tank by 12 itself. When both pipes are
open the tank fills in 4 minutes 48 seconds. How long does it take the large
pipe acting alone to drain the tank?
23.The pressure of a gas , P, varies directly as the temperature, T, and inversely as the volume, V . In the problems below give all results to three significant digits. If P is 1.10 atm (atmosphere) when T = 300K and V = 22.0l , what is V when T = 450K and P =1.70 atm ?
24. For fixed electrical charge, the capacitance of a pair of charged
parallel circular plates varies directly as the square of the
plate radius and inversely as the plate separation. If the capacitance is 34.7μF
(micro farads) when the plate radius is 1.0 cm
and the plate separation is 4.0μm (microns, 1μm = 0.0001 cm), what is the
plate separation, if for the same amount of
charge and a plate radius of 2.0 cm the capacitance is 347.0μF ?
25. The resistance, R , of a wire varies directly as the length,
l , and
inversely as the diameter, d , squared. If R = 3.50Ω
when l = 10.0m and d = 0.125 cm , what is the resistance of a wire made of the
same material that is 5.00m long and has
a diameter of 0.250 cm ? (Give the answer to 3 significant digits.)
Intermediate Algebra 2 : Project 3 (Chapter 7)
Problems 1 through 26 are each worth 1 point. Problems 27 through 38 are each
worth 2 points.
Simplify the following using only positive rational exponents.
1.
2.
3.
4.
5.
6.
7.
Express the following numbers in scientific notation as numbers between 1 and 10
times the appropriate power of 10.
8.
9.
10.
11.
12.For x > 0,
Express the following using only positive rational exponents.
13.
14.
Express the following in radical notation reduced to simplest radical form with rationalized denominators.
15.
16.
Simplify the following expressing all answers in simplest radical form with
rationalized denominators.Assume for even
roots that all variables represent positive numbers.
17.
18.
19.
20.
21.
22.
23.
24.
Simplify the following giving the correct answer for any real value of x
25.
26.
Simplify the following complex numbers, expressing the result in standard form a + bi.
27.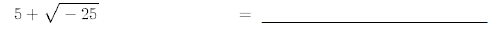
28.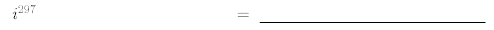
29.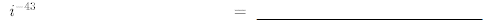
30.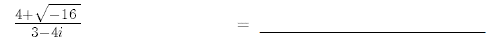
31.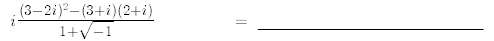
Solve the following equations for all real roots.
32.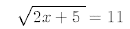
33.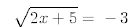
34.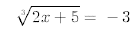
35.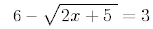
36.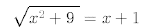
37.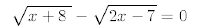
38.Use Winplot and attach the computer plot or sketch the results below. Use
the window :
left = down = -0.5; right = up = 4 . The function sqrt stands for the square
root function.
Check "lock interval" to fix the domain as stated. To generate the "correct"
shape of the curves
select Zoom/Square from the View menu.
| Equa format | Domain | formula | |
| Curve 1. | y=f(x) | low x = 0 ! high x = 4 |
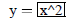 |
| Curve 2. | y=f(x) | low x = 0 ! high x = 4 |
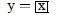 |
| Curve 3. | x=f(t) | low t = 0 ! high t = 4 |
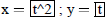 |
| Curve 4. | y=f(x) | low x = 0 ! high x = 4 |
 |
| Curve 5. | x=f(t) | low t = 0 ! high t = 4 |
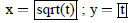 |
a)What is true about the line y=x (Curve 2) , with respect to Curve 1 and
Curve 3?
b)How do the Curve 1 and Curve 5 compare ? Explain why this is not surprising.
c)How do the Curve 3 and Curve 4 compare? Explain why this is not surprising.
Intermediate Algebra 2 : Project 4 (Chapter 8)
Problem 1 through 28 are each worth 1.5 points. Problems 29 and 30 are each
worth 4 points.
1. Solve the following equation by factoring.
12x2-7x-10=0
2. Solve the following equation by completing the square.
2x2-8x+26=0
3. Solve the following equation by completing the square.
3x2+9x+18=0
Solve the following equations for all real and/or complex roots by any method.
4. 4x2-8x-21=0
5. 3x2-12x=x2-26
6. x3-4x=2x2
7.
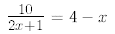
8.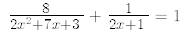
Solve the following for all real roots.
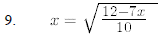
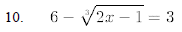
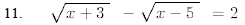
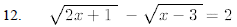
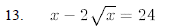
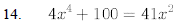
15. For what values of does the equation have 2x2-5x+c=0 two distinct real roots?
16. A storage tank has two inlet pumps. The smaller pump takes 20 minutes longer by itself to fill the tank than does the larger pipe. When both pumps are running the tank fills in 24 minutes. How long does it take the large pump acting alone to fill the tank?
17. Mary and Steve each travel 420 miles. Mary drove an average of 10 mph faster than Steve and completed the trip in one hour's less time than Steve. What was each person's average speed?
Graph the following functions. If the graph is a parabola give the coordinates of the vertex and the equation of the axis of symmetry.
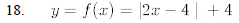
19.y = f(x) = 6-x2
20.y = f(x) = x2-4x+3
21.y = f(x) = 1-2x2+6x
22.x = f(y) = -6-3y2-12y
Write an equation which generates each of the following curves.
23. A circle of radius & centered at (- 4,2) .
24. A parabola with vertex at(- 5,3), axis of symmetry x = - 5 , and passes through the point (1,-23)
25. A parabola with vertex at (2¸-1) , axis of symmetry y = -1 , and passes through the point (4,0)
Solve and graph the solution set of the following inequalities.
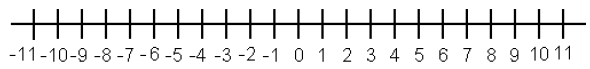
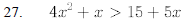
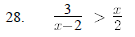
29. Using the WinPlot program graph the function
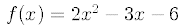 for
for
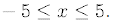
Hand in the computer graph with your assignment. From your graph estimate the
two roots of f(x).
root #1 = _____________
root #2 = _____________
Now calculate 'exactly' the two roots of f(x).
root #1 = _____________
root #2 = _____________
30.Using the WinPlot program graph the function
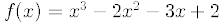 for
for
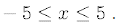
Hand in the computer graph with your assignment. From your graph estimate the
three roots of f(x) .
root #1 oe _____________
root #2 oe _____________
root #3 oe _____________
Intermediate Algebra 2 : Project 5 (Chapter 9)
Problems 3, 4, 5 and 10 are each worth 4 points. Problems 8 and 9 are each worth 3 points. All other problems are each worth 2 points.
1. Use WinPlot and attach the computer plot or sketch the results below. Use the
window : left = down = -5
right = up = 5 . To generate the "correct" shape of the curves select Zoom
square from the View menu
| Equa format | Domain | formula | |
| Curve 1. | y=f(x) | low x = -5 ! high x = 5 |
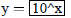 |
| Curve 2. | y=f(x) | low x = -5 ! high x = 5 |
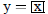 |
| Curve 3. | x=f(t) | low t = -5 ! high t = 5 |
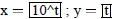 |
| Curve 4. | y=f(x) | low x = -5 ! high x = 5 |
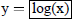 |
| Curve 5. | x=f(t) | low t = -5 ! high t = 5 |
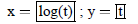 |
a)What is true about the line y oe x , with respect to the Curve 1 and Curve 3?
b)How do the Curve 1 and Curve 5 compare? Explain why this is not surprising.
c)How do the Curve 3 and Curve 4 compare? Explain why this is not surprising.
2. Use WinPlot and attach the computer plot or sketch the results below. Use the
window : left = down = -5 ; right = up = 5 .
To generate the "correct" shape of the curves select Zoom square from theView
menu.
| Equa format | Domain | formula | |
| Curve 1. | y=f(x) | low x = -5 ! high x = 5 |
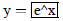 |
| Curve 2. | y=f(x) | low x = -5 ! high x = 5 |
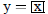 |
| Curve 3. | x=f(t) | low t = -5 ! high t = 5 |
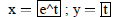 |
| Curve 4. | y=f(x) | low x = -5 ! high x = 5 |
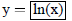 |
| Curve 5. | x=f(t) | low t = -5 ! high t = 5 |
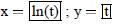 |
a)What is true about the line y oe x , with respect to the Curve 1 and Curve 3?
b) How do the Curve 1 and Curve 5 compare? Explain why this is not surprising.
c) How do the Curve 3 and Curve 4 compare? Explain why this is not surprising.
3. Given f(x) = 2x + 1 and 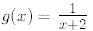
a)What is the domain of f?
b)What is the range of f ?
c)What is the domain of g ?
d)What is the range of g ?



4. Using the functions f(x) and g(x) defined in problem 3, find the inverse functions
5. For the functions f(x) and g(x) defined in problem 3 and the inverse functions of problem 4,
a)What is the domain of f -1? "
b)What is the range of f -1? "
c)What is the domain of g -1? "
d)What is the range of g -1?

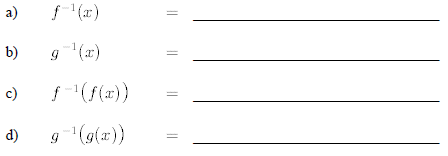
For the following functions :
i) State the domain
ii) State the range
iii) Sketch the curve
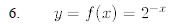
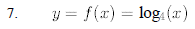
8. Change the following expressions from exponential form to logarithmic form :
a) 109 = 1000000000
b) 210 = 1024
c) A = er
d) 2-3 = 0.125
e) 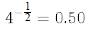
f) ab = c
9. Change the following from logarithmic to exponential form:
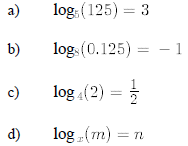
10. Compute the following
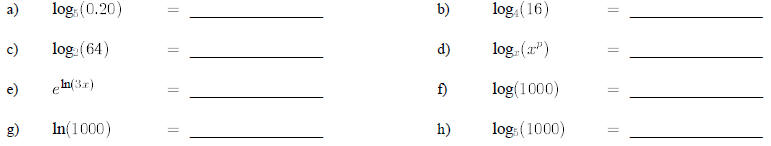
Solve the following equations for all real roots. If no real solution exists,
write 'No Solution' . You may leave answers in a form which involves an
irrational base-10 or natural logarithm. For example,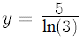 or you may give
the numerical
or you may give
the numerical
answer y = 4.551196133… Each problem is worth 1 point.





16.ln(x) 2


19. The decay of a radioactive material is expressed by
the function
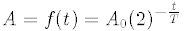 where
A is the amount of material
where
A is the amount of material
left after a time t has elapsed, A0 is the starting amount of
material, and X is the half-life of the material. If in 1500 years time, 20% of the material
decays (leaving 80% of the material still present), what is the half-life?
20. Four thousand dollars is deposited in a savings account with a fixed yearly interest rate of 3.75%.
a) After five years how much money is in the account if the it is compounded quarterly ?
b) After five years how much money is in the account if the it is compounded continuously?
c) In this situation how much money does continuous compounding gain versus quarterly compounding?
d) If the account is compounded quarterly, how many years would it take for the amount to reach $6000.00?
Instructions for the Group Lab: The Simple Pendulum
The following guidelines should be adhered to in forming your lab group, performing the experiments, and writing up the labs.
Group Requirements:
Each group must consist of at least two individuals but no more than four
individuals. You are free to form your own groups, but if you
can't find a partner see me and I'll assign you to a group. Two class periods
will be devoted to doing each lab, but probably some of the
report writing will have to be done outside of class. It is up to the group to
decide any internal division of labor, eg., who is responsible
for data observation and or recording, who will do the algebra, who will check
the work, who will write up the what parts of the report.
It is possible that in one group a single individual writes the entire report,
while in another group everyone writes up a different part .
It is in your own best interest to insist that you understand the entire lab
report. You are free to use any written resources or computing
technology in doing your analysis.
Report Requirements:
Each group must hand in report for a given lab which should one include the
following :
1. The names of all group participants. If the report writers feel an individual
did not perform his/her assigned task, you are free to delete
that person's name from the report. I will arbitrate all appeals on such
disagreements and reserve the right to give either a written or oral
exam to decide the issue.
2. The conclusions stated neatly in sentences which are both concise and
complete.
3. The work attached in a way which is both neat and clear. Answers should be
presented in the same order as the associated questions .
Grading:
1. Each person in the group will receive the same point total out of 40 that the
lab report receives. Appeals on this are permitted, but I
reserve the right to then administer either an oral or written exam to such an
individual to replace the group score. Thus, it is the
responsibility of everyone in the group to review the analysis, conclusions and
answers to all of the questions.
2.Grades will be based on both the quality of the data taken and the correctness
of the methods used to analyze the data. Thus, a correct
conclusion arrived at by accident using faulty mathematics will not count for
much. Points will be deducted for incomplete, illegible, sloppy
or incomprehensible answers.
Intermediate Algebra Lab: The Simple Pendulum
Purpose : To investigate the relationship between the length of a simple pendulum and the time it takes to complete a full swing.
Equipment : String, stop watch, weights, meter stick, protractor, ( a balance if available).
General Procedure : Tie one of the weights to the end of the string. From the
center of the weight measure off the specified
length of the string. Holding the string at this distance, let the lead weight
swing P freely from an initial position that makes a 20°
angle (θ = 20°) with the vertical . Measure the time for 10 full swings of the
weight. Divide this time by 10 to obtain the period, T ,
the time for one full swing. Repeat this procedure for each of the specified
values of L . Then repeat the experiment for ) θ= 25°
and ) θ = 30° Finally, pick a second, different mass weight and repeat the
entire set of measurements.
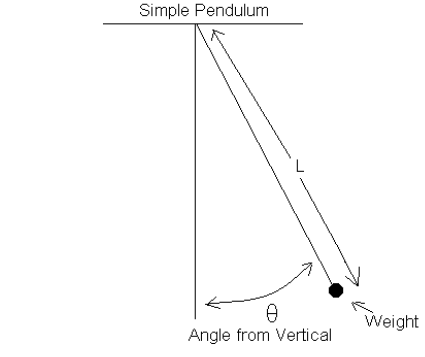
I. Data Collection (16 points)
Data Table for First Weight ( If Balance available mass of weight = __________ )
| θ = 20° | θ = 25° | θ = 30° | ||||
| L | Time for 10 Swings | Period T | Time for 10 Swings | Period T | Time for 10 Swings | Period T |
| 10.0cm | ||||||
| 15.0cm | ||||||
| 20.0cm | ||||||
| 25.0cm | ||||||
| 30.0cm | ||||||
| 35.0cm | ||||||
| 40.0cm | ||||||
| 45.0cm | ||||||
| 50.0cm | ||||||
| 55.0cm | ||||||
| 60.0cm | ||||||
| 65.0cm | ||||||
| 70.0cm | ||||||
| 75.0cm | ||||||
| 80.0cm | ||||||
Data Table for Second Weight ( If Balance available mass of weight = __________ )
| θ = 20° | θ = 25° | θ = 30° | ||||
| L | Time for 10 Swings | Period T | Time for 10 Swings | Period T | Time for 10 Swings | Period T |
| 10.0cm | ||||||
| 15.0cm | ||||||
| 20.0cm | ||||||
| 25.0cm | ||||||
| 30.0cm | ||||||
| 35.0cm | ||||||
| 40.0cm | ||||||
| 45.0cm | ||||||
| 50.0cm | ||||||
| 55.0cm | ||||||
| 60.0cm | ||||||
| 65.0cm | ||||||
| 70.0cm | ||||||
| 75.0cm | ||||||
| 80.0cm | ||||||
Give a brief but accurate description of the procedure you followed in obtaining your data. Use diagrams where necessary and identify all pertinent variables.
II. Data Analysis (16 points) ( Feel free to use a spreadsheet to perform the required calculations and plot the graphs. )
What were the relevant variables in this experiment?
Which variables were independent and which were dependent?
Construct a graph of T versus L . Label all axes and label each curve as to
the weight and angle (θ) used. You may if you wish put all
six curves on the same graph. You may use either the grid provided or your own
graph paper.
In general, how did the period depend on the initial angle θ?
In general, how did the period depend on the weight used ?
Graphs of T versus L
Construct a graph of ln(T) versus ln(L). Label all axes and label each curve as to the weight and angle (θ) used. You may if you wish put all six curves on the same graph. You may use either the grid provided or your own graph paper. Record the data for these graphs in the table provided.
- Ln(T) and Ln(L) Data
| Ln(T) and Ln(L) Data for First Weight | Ln(T)Data for Second Weight | ||||||
| Ln(T) | Ln(T) | ||||||
| L | ln(L) | θ = 20° | θ = 25° | θ = 30° | θ = 20° | θ = 25° | θ = 30° |
| 10.0cm | |||||||
| 15.0cm | |||||||
| 20.0cm | |||||||
| 25.0cm | |||||||
| 30.0cm | |||||||
| 35.0cm | |||||||
| 40.0cm | |||||||
| 45.0cm | |||||||
| 50.0cm | |||||||
| 55.0cm | |||||||
| 60.0cm | |||||||
| 65.0cm | |||||||
| 70.0cm | |||||||
| 75.0cm | |||||||
| 80.0cm | |||||||
Graphs of ln(T) versus ln(L)

III. Interpretation (14 points)
Is the relationship between T and L linear? Explain your answer
Is the relationship between ln(T) and ln(L) linear? Explain your answer
From elementary physics the period of a simple pendulum for small initial
angles satisfies a ' power law ' relationship to the length.
That is T = A·Lp. Where A is a constant independent of
L. From your data
obtain an estimates of p and A. Explain how you obtained
these estimates.
Hint: The"best" or regression fit of a straight line through a set of
n data
points (xi,yi) is given by he linear model t y = mx + b ,
where m is the slope and b is the y intercept. The slope of the regression line
is given by
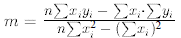 while the
y intercept can be calculated as
while the
y intercept can be calculated as
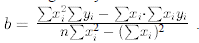 .
.
Here we are using summation notation where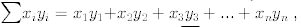
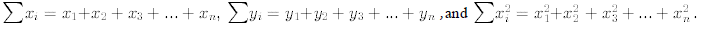
Estimated value of : p= _____________ Estimated value of A= _____________
For the same weight you used estimate the period if L =
100 cm . If you have
the equipment you may wish to check this estimate by
actually measuring the period.
Estimated period for a length of 100 cm=_____________
IV. Application (4 points)
Below is a table of data on the electrical resistance,R, for a 1 meter length of
different copper wire. The wire's diameter is d .
Copper Wire Resistance Data
| Gauge | d(cm) | 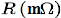 |
| 30 | 0.03175 | 223.7 |
| 25 | 0.05556 | 73.0 |
| 20 | 0.09525 | 24.9 |
| 15 | 0.1786 | 7.1 |
| 12 | 0.2778 | 2.9 |
| 10 | 0.3572 | 1.8 |
| 9 | 0.3969 | 1.4 |
| 8 | 0.4366 | 1.2 |
| 7 | 0.4763 | 1.0 |
| 6 | 0.5159 | 0.8 |
| 5 | 0.5556 | 0.7 |
| 4 | 0.5953 | 0.6 |
According to theory the resistance is related to diameter by a 'power law' . That is R = A·dp . where A is a constant independent of d. From the table obtain an estimate of p. Explain how you obtained this estimate.
Estimated value of : p= _____________ Estimated value of A= _____________
Estimate the resistance for a 1 meter length of 35 gauge copper wire (d = 0.01984cm) .
Estimated resistance for a 1 m length of 35 gauge copper wire = _____________

Intermediate Algebra 2 : Project 6 (Chapter 4)
Each problem is worth 2 points.
1. Let L be the line that passes through (-3,5) and is parallel to the line 5x -
4y = -18.
Let M be the line that passes through (-3,5) and is perpendicular to the line 5x
- 4y = -18 .
Equation of L in slope-intercept form : _____________________
Equation of M in slope-intercept form : _____________________
The B intercept of L = ____________ The B intercept of M = ____________
The C intercept of L = ____________ The C intercept of M = ____________
The slope of L = ____________ The slope of M = ____________
Graph the lines L and M
2. Plot each line to find the solution of the system of equations:
x + 3y = -7
2x - y = 7
Then check your answer by solving the system algebraically
3. Graph the solution set of the inequality :-4y + 6x < 24
4.Using the WinPlot program . graph the two linear
functions y = f(x) = 2x + 3 and y = f(x) = -2x + 1
from low x = -5 to high x = 5. Hand in the computer graph with your
assignment. From the graph estimate the point of
intersection of the two lines. Then algebraically solve the system of equations
which corresponds to this intersection.
Point of intersection = ____________
Solve the following systems of equations algebraically.
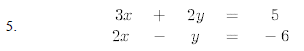
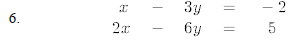
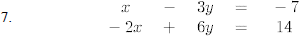
8. A man travels 620 miles by both train and bus. The bus averages
60 mph, while the train averages 40 mph. The total travel
time on both train and bus was 12 hours. How long did the bus trip last?
9. How many grams of pure tin must be mixed with 200 g of
25% tin solder and 100
g of 30% tin solder in order to have a
final solder which is 40% tin?
10. Mary delivers one less package than twice as many as Terri. Together Terri
and Kevin deliver five more packages than Mary.
All together the three of them deliver fifty-one packages. How many packages are
delivered by each person?
11. Joan has $1.76 in change. She has four less dimes than
pennies, but one more dime than twice the number of quarters.
She also has one more nickle than quarters. How many of each kind of coin does
Joan have?
Solve and classify (consistent and independent,
inconsistent, or dependent) the following systems of equations .
If the solutions are dependent, give the linear "form" of the infinite number of
solutions.





17. In WinPlot open the 3-dim window and solve each of the
following three equations for z. Enter each formula for z as an Explicit
function in Equa/Explicit menu. From View pick Axes to get a better 3D
perspective of the surfaces. Be sure to use a different color
for each surface. This is chosen under color of the Equa/Explicit menu. Solve
this system of equations and enter the coordinates of
the solution using the Equ/Point/Cartesian menu. Be sure the color of this point
is distinct from the color of the three surfaces.
Use PgUp (or the View Memu) to "zoom in" and the left and right arrow keys to
rotate the graph until you get a "good view"
which clearly shows the three surfaces and the solution point. Print and attach
your graph.
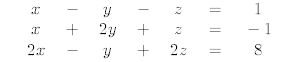
What kind of geometric surfaces does each equation describe?
What is the significance of the solution point with respect to the three surfaces?
18. In WinPlot open the 3-dim window and solve each of the following three
equations for z. Enter each formula for z as an Explicit
function in Equa/Explicit menu. From View pick Axes to get a better 3D
perspective of the surfaces. Be sure to use a different color
for each surface. Show that this system is consistent but dependent with
infinitely many solutions along a line. Determine the form
of this solution. In this form let z = t where t is any real number. Solve for
x and y in terms of t. In WinPlot use the Equa/Curve
menu to enter the form of the infinetly many solutions. Set t lo = -5 and t hi =
5. Set the pen width to 2 and choose a dominant
color to make this line more prominent. Use Use PgUp (or the View Memu) to "zoom
in" and the left and right arrow keys rotate the
graph until you get a "good view" which clearly shows the three surfaces and the
line of solutions. Print and attach your graph.
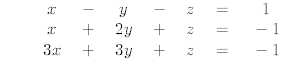
What kind of geometric surfaces does each equation describe?
What is the significance of the line of solutions with respect to the three surfaces?
Evaluate the following determinants.
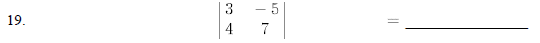
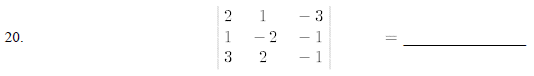
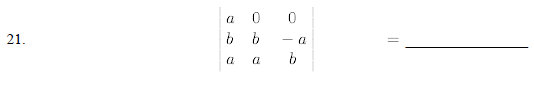
Solve the following systems of equations by Cramer's Rule

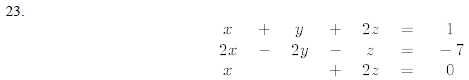
24. Graph the solution set of the system of inequalities:
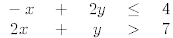
25. Graph the solution set of the system of inequalities
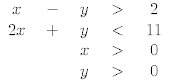
| Prev | Next |