Integration of Rational Functions by Partial Fractions
1. The method of partial fractions is used to replace a
complex rational
function (in reduced form ) with a sum of simpler rational functions.
These simpler rational functions will be easier to integrate.
2. Let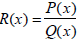 
be a rational
function. Thus, P(x) and Q(x) are
polynomials.
3. The method of partial fractions lets us write
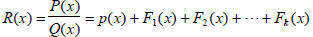
were p(x) is a polynomial and each F i(x) is a
rational function of the
form:
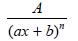or
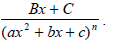
The two rational expressions above are called partial fractions and
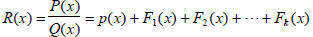
is called the partial fraction decomposition of R(x).
4. Method: Find the partial fraction decomposition
of
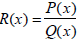
a. If the degree of P(x) is greater than or equal to
the degree
of Q(x), use long division to divide P(x) by Q(x). (If the
degree of Q(x) is larger, then go to the next step.)
1. Be sure to express each polynomial P and Q in
descending powers of x .
2. The quotient ( result of the division ) is the polynomial p(x)
in the partial fraction decomposition.
3. The remainder has a degree less than the degree of the
devisor Q(t).
4. This will reduce R(x) to the form:
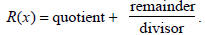
5. Proceed with the next steps on the rational expression
, which will have the numerator with a
smaller
degree than the denominator. (In the remainder of the
method, we will now refer to this rational expression as
P (x)/Q(x).)
b. Factor the denominator Q(x) into linear and quadratic
factors, possibly repeated.
1. Linear factors will have the form ax + b; or, if repeated
n times, the form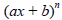 
.
2. Quadratic factors will have the form ax2 + bx + c, where
this quadratic polynomial cannot be factored further over
the real numbers . (b2 − 4ac < 0 ) If this factor is
repeated m times the form will be
.
3. This can always be done theoretically because any
polynomial of degree N has N real or complex roots,
possibly repeated. If the polynomial has real
coefficients, the real roots give the linear factors and the
complex roots give the quadratic factors (with real
coefficients).
c. The linear factors 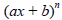of the
denominator lead to
partial fractions of the form:
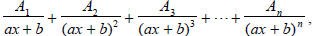
were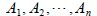 
are all constants
to be determined, some
of which could be zero. (There will be one set of n such
fractions for each linear factor of the form .)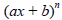
d. The quadratic factors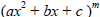
of the denominator
lead to partial fractions of the form:
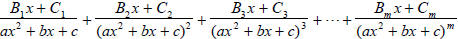
where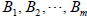 
and
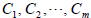are all constants to
be determined some of which could be zero. (Again one set of
m for each factor of the form
.)
e. The partial fraction decomposition of P(x)/Q(x) (assuming the
degree of Q(x) is larger than the degree of P(x)) is then the
sum of all of the these partial fractions related to all of the
linear and quadratic factors of the denominator Q (x).
f. There are two method for determining the constants.
Both methods start by multiplying both sides of the partial
fraction decomposition by the denominator of the original
rational function. This will clear all denominators. The
resulting equation (called the basic equation) will be true for
all values of x .
1. Since the basic equation is true for all values of x,
substitute a value for x that simplifies the equation. For
a distinct linear factor, pick x = the zero of this factor.
This will to eliminate most of the unknown constants in
the basic equation. Solve. Repeat for all distinct linear
factors.
2. Expand the basic equation and collect terms according to
their power of x. Equate coefficients of like powers of x
to obtain a system of linear equations involving the
unknown constants. Solve this system of equations.
3. A combination of these two methods is often the most
efficient method of finding these missing constants.
5. In Mathematica , a rational expression can be written in its partial
fraction decomposition using the command Apart.
6. The rational function written in the form of its partial fraction
decomposition will be easier to integrate. For example:
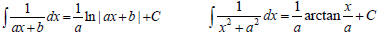
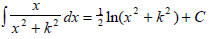
For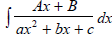
complete
the square in the denominator.
| Prev | Next |