Example of Extended Euclidean Algorithm
Recall that gcd(84, 33) = gcd(33, 18) = gcd(18, 15) =
gcd(15, 3) = gcd(3, 0) = 3
We work backwards to write 3 as a linear combination of
84 and 33:
3 = 18 − 15
[Now 3 is a linear combination of 18 and 15]
= 18 − (33 − 18)
= 2(18) − 33
[Now 3 is a linear combination of 18 and 33]
= 2(84 − 2 × 33)) − 33
= 2 × 84 − 5 × 33
[ Now 3 is a linear combination of 84 and 33]
Some Consequences
Corollary 2: If a and b are relatively prime, then there
exist s and t such that as + bt = 1.
Corollary 3: If gcd(a, b) = 1 and a | bc, then a | c.
Proof:
• Exist s, t ∈ Z such that sa + tb = 1
• Multiply both sides by c: sac + tbc = c
• Since a | bc, a | sac + tbc, so a | c
Corollary 4: If p is prime and
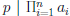 , then p | ai
, then p | ai
for some 1≤ i ≤ n.
Proof: By induction on n:
• If n = 1: trivial.
Suppose the result holds for n and
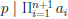 .
.
• note that
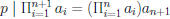 .
.
• If
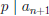 we are done.
we are done.
• If not,
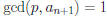 .
.
• By Corollary 3,
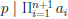
• By the IH, p | ai for some 1 ≤ i ≤ n.
The Fundamental Theorem of
Arithmetic , II
Theorem 3: Every n > 1 can be represented uniquely
as a product of primes , written in nondecreasing size.
Proof: Still need to prove uniqueness. We do it by strong
induction.
• Base case: Obvious if n = 2.
Inductive step . Suppose OK for n' < n.
• Suppose that 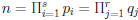
• 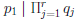 , so by Corollary 4,
, so by Corollary 4,
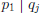 for some j.
for some j.
• But then 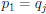 , since both
, since both
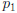 and
and 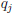 are
prime.
are
prime.
• But then 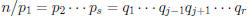
• Result now follows from I.H.
Characterizing the GCD and LCM
Theorem 6: Suppose 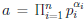 and
and
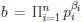 ,
,
where pi are primes and 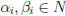 .
.
• Some 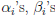 could be 0.
could be 0.
Then
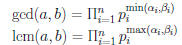
Proof: For gcd, let 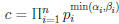 .
.
Clearly c | a and c | b.
• Thus, c is a common divisor , so c ≤ gcd(a, b).
If 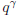 | gcd(a, b),
| gcd(a, b),
• must have 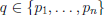
o
Otherwise q 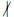 | a so q
| a so q
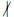 | gcd(a, b) ( likewise b )
| gcd(a, b) ( likewise b )
If 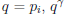 | gcd(a, b), must have
| gcd(a, b), must have
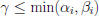
o E.g., if
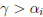 , then
, then 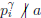
• Thus, c ≥ gcd(a, b).
Conclusion: c = gcd(a, b).
For lcm , let 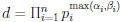 .
.
• Clearly a | d, b | d, so d is a common multiple .
• Thus, d ≥ lcm(a, b).
Suppose 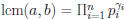 .
.
• Must have
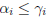 ,
since
,
since
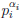 | a and a | lcm(a, b).
| a and a | lcm(a, b).
• Similarly, must have 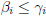 .
.
• Thus, 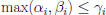 .
.
Conclusion: d = lcm(a, b).
Example: 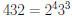 , and
, and
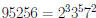 , so
, so
• 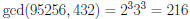
• 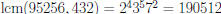 .
.
Corollary 5: ab = gcd(a, b) · lcm(a, b)
Proof:
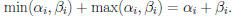
Example: 4 · 10 = 2 · 20 = gcd(4, 10) · lcm(4, 10).
Modular Arithmetic
Remember: a ≡ b (mod m) means a and b have the same
remainder when divided by m .
• Equivalently : a ≡ b (mod m) iff m | (a − b)
• a is congruent to b mod m
Theorem 7: If 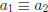 (mod m) and
(mod m) and
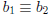 (mod m),
(mod m),
then
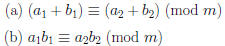
Proof: Suppose
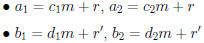
So
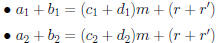
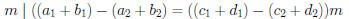
• Conclusion: 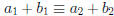 (mod m).
(mod m).
For multiplication:
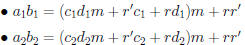
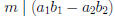
• Conclusion: 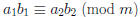 .
.
Bottom line: addition and multiplication carry over to
the modular world.
Modular arithmetic has lots of applications.
• Here are four . . .
Hashing
Problem: How can we efficiently store, retrieve, and
delete records from a large database?
• For example, students records.
Assume, each record has a unique key
• E.g. student ID, Social Security #
Do we keep an array sorted by the key?
• Easy retrieval but difficult insertion and deletion.
How about a table with an entry for every possible key?
• Often infeasible, almost always wasteful.
• There are 1010 possible social security numbers.
Solution : store the records in an array of size N, where N
is somewhat bigger than the expected number of records .
• Store record with id k in location h(k)
o h is the hash function
o Basic hash function: h(k) := k (mod N).
• A collision occurs when 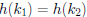 and
and
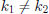 .
.
o Choose N sufficiently large to minimize collisions
• Lots of techniques for dealing with collisions
| Prev | Next |