Counting Factors, Greatest Common Factor , Least Common Multiple

•Every number can be expressed in terms of primes
i.e. 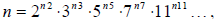where n2, n3, n5, n11 are integer exponents (maybe 0)

•Example. Express 144 in terms of its prime factorization
144 = 2⁴ •3² . So n2 = 4, n3 = 2, and all the others are 0
•The number of factors for a given whole number is related to the exponents in its prime
factorization. The number of factors = (n2 +1)(n 3+1)(n 5+1)…

•Example. How many factors are there for 144?
Since the factorization for 144 is 2⁴ •3² , there are (4+1)(2+1) = 15 different factors for 144
•You find these factors by taking all possible combinations of the prime factorization with exponent
values from 0 to n2, 0 to n3, 0 to n5, etc

•Example. What are the factors of 144?

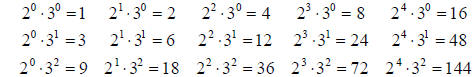
•Example, page 208 number 1d. How many factors does 12⁴ have?
12⁴ = (2² •3)⁴= 2⁸•3⁴. It has (8+1)(4+1) = 45 factors

•Example, page 208 number 2a. Factor 120 into primes
120 = 60 •2 = 30•2² = 10 •2² = 5•3•2³

The Greatest Common Factor:
•The greatest common factor (GCF) of two (or more) nonzero whole numbers is the largest whole
number that is a factor of both (all) of the numbers
•You can find the greatest common factor by the set intersection method
-Finding all factors of each of the numbers and placing them in sets
-Finding the intersection of those sets
-Finding the largest value in the intersection

•Example, page 208 number 6d. Find the GCF(42, 385)
Factors of 42:

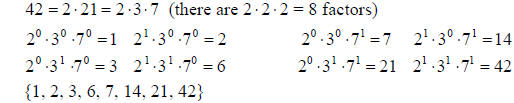
Factors of 385:

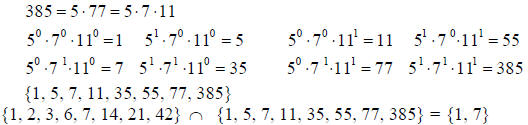
GCF(42, 385) = 7

•You can also find the GCF by the prime factorization method
-Find the prime factorization of each number
-Take whatever they have in common (to the highest power possible )

•Example, page 208 number 6d. Find the GCF(42, 385)
Factorization 42 = 2•1= 2•3•7
Factorization 385 = 5•7 = 5• 11
GCF(42, 385) = 7¹ = 7

•Example, page 208 number 6f. Find the GCF(338, 507)
Factorization 338 = 2•69 = 2 •3²
Factorization 507 = 3•69 = 3•3²
GCF(338, 507) = 13² = 169

•If a and b are whole numbers with a ≥ b , then GCF(a, b) = GCF(a - b, b)

•Example, page 208 number 6f (again)
GCF(507, 338) = GCF(507 - 338, 338) = GCF(169, 338)

Least Common Multiple:
•The least common multiple (LCM) of two (or more) nonzero whole numbers is the smallest
nonzero whole number that is a multiple of each (all) of the numbers

•You can find the least common multiple with the set intersection method
-List the nonzero multiples of each number
-Intersect the sets
-Take the smallest element in the intersection

•Example, page 208 number 7d. Find the LCM(66, 88)
Multiples of 88 {88, 176, 264, 352…}
Multiples of 66 {66, 132, 198, 264, 330…}
LCM(66, 88) = 264

•You can also find the LCM with the prime factorization method (similar to the buildup method)
-Express the numbers in their prime factorization
-Take each factor (to its highest power ) from each factorization, but do not repeat

•Example, page 208 number 7d (again)
88 = 2 •44 = 2² •2²= 2 ³•11
66 = 3•2 = 2•11
LCM(66, 88) = 2³ •11 = 264