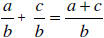THE SET OF RATIONAL NUMBERS
I. ADDITION WITH “ LIKE ” DENOMINATORS
 |
 |
 |
||
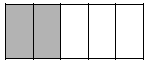
| 1/5 | + | 2/5 | = |
So,1/5 + 2/5 =
II. ADDITION WITH “ UNLIKE ” DENOMINATORS
But what if the fractions do not have the same
denominator?
For instance,1/3 + 1/4

But, how do we count this? We need to find a way to
combine the two drawings to find the sum.
Let’s “build-up” each fraction:
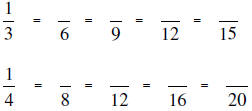
Now, compare these two lists and look for a “like”
denominator . What is it? ________

If a/b and c/d are any two rational numbers, then
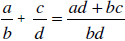
| EXAMPLES: | Using the LCD | Using the Above Property |
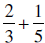 |
||
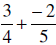 |
||
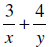 |
||
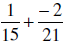 |
III. MIXED NUMBERS
Mixed numbers are numbers that are the sum of an integer and a fractional
part of an integer. For
example, if a nail is 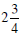 inches long, this
means 2 inches plus an additional 3/4 inches. (It is
inches long, this
means 2 inches plus an additional 3/4 inches. (It is
common to think that since 2y means 2 times y, that
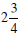 means 2 times3/4, but this is
incorrect!)
means 2 times3/4, but this is
incorrect!)
Change the following mixed numbers to improper fractions.
| Using the Coventional Algorithm | Change with Meaning |
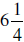 |
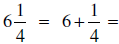 |
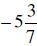 |
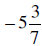 |
Change the following improper fractions to mixed numbers.
| Using the Coventional Algorithm | Change with Meaning |
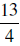 |
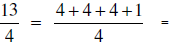 |
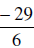 |
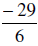 |
IV.
Given any two rational numbers a/b and c/d where , b and d
are non- zero integers :
1. Closure
2. Commutative
3. Associative
4. Additive Identity
5. Additive Inverse
For any rational number a/b there exists a unique
number ________ such that:
Name the additive inverse of the following:
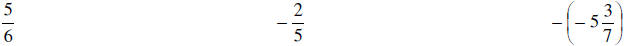
V. ADDITION OF MIXED NUMBERS (Know how to add using the given mixed numbers)
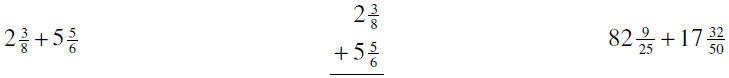
VI. SUBTRACTION OF RATIONAL NUMBERS
If a/b and c/d are any rational numbers, then
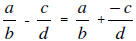
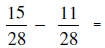
If a/b and c/d are any two rational numbers, then
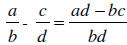
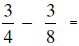
SUBTRACTION OF MIXED NUMBERS (Know how to subtract using the given mixed numbers
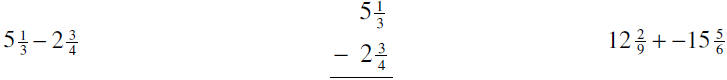
VII. ESTIMATION WITH RATIONAL NUMBERS
Many times when estimating with fractions, it is helpful
to round to a convenient fraction –
for instance:0,1/2,1/3,1/4,1/5,2/3,3/4,or 1.
For example, if you got 59 out of 80 questions correct on your test, this is about 60/80 or 6/8 or 3/4
Then we can conclude that 3/4 is a HIGH ESTIMATE.
(You actually got less than 3/4 of the test correct, since 59 < 60, then 59/80< 60/80 = 3/4).
Approximate each of the following using 0,1/4,1/3,1/2,3/4,or 1.Tell if your estimate is low or high .
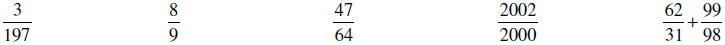
| Prev | Next |