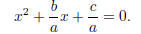The Quadratic Formula
The quadratic formula is a formual for finding the
roots of a quadratic equation. It depends on a
procedure called completing the square. Here’s the idea. Suppose you can
do algebra to get your equation
to look like this :
(variable-stuff)2 = (a number).
Then you can solve for the variable -stuff by taking the square root of both
sides.
Example. Solve the equation for x.
(a) x2 − 49 = 0.
x2 − 49 = 0
x2 = 49
x = ±7
(b) x2 + 16 = 0.
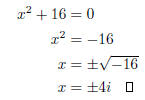
(c) (x − 5)2 = 4.
(x − 5)2 = 4
x − 5 = ±2
x − 5 = 2 gives x = 7 and x − 5 = −2 gives x = 3. The solutions are x = 7 and x = 3.
Suppose you start out with a quadratic equation where you
don’t have a perfect square on one side.
Suppose, for instance, that the variable-stuff is x2 + ax.
What would you need to add to x 2 + ax to make it a perfect square? If
it comes from (x + c)2 =
x2 + 2cx + c2, then the middle (x) terms must be the same.
So
2cx = a, c =a/2.
Therefore, I need to add
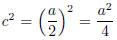 to get a perfect square. The procedure is:
Take half of the
to get a perfect square. The procedure is:
Take half of the
coefficient of the middle term
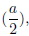 then square it
then square it 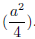
Example. Solve x2 + 6x = 16 by
completing the square.
The x term is 6x. Half of 6 is 3, and 32 = 9. Therefore, I should add
9 to both sides:
x2 + 6x = 16
x2 + 6x + 9 = 25
(x + 3)2 = 25
x + 3 = ±5
x + 3 = 5 gives x = 2; x + 3 = −5 gives x = −8. The
solutions are x = 2 and x = −8.
Example. Solve x2 − 10x = 16 by completing the square.
The x term is −10. Half of −10 is −5, and (−5)2 = 25. Therefore, I
should add 25 to both sides:
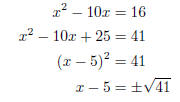
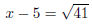 gives
gives 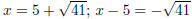 gives
gives 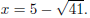 The solutions are
The solutions are
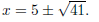
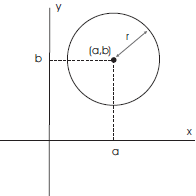
As an application of completing the square, I’ll look at equations of circles.
The standard form for the
equation of a circle with radius r and center (a, b) is
(x − a)2 + (y − b)2 = r2.
Example. (a) Find the center and radius of the
circle whose equation is
(x − 5)2 + (y + 3)2 = 36.
The center is (5,−3) and the radius is 6.
(b) What is the equation of the circle whose center is
(−4, 8) and whose radius is 1.1?
(x − (−4)2 + (y − 8)2 = 1.12, or (x + 4)2
+ (y − 8)2 = 1.21.
(Don’t multiply out the left side — leave it as is.)
You can find the center and radius of a circle whose
equation is not in standard form by completing the
square.
Example. Find the center and radius of the circle
x2 − 2x + y2 + 6x = 15,
To complete the square in x, I have −2/2= −1, and (−1)2
= 1. To complete the square in y, I have
6/2= 3, and 32 = 9. So I have
x2 − 2x + 1 + y2 + 6x + 9 = 15 + 1 + 9, or (x − 1)2
+ (y + 3)2 = 25.
The center is (1,−3) and the radius is 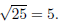
Now I’ll see how to use completing the square to obtain a
formula for solving an aribtrary quadratic
equation.
Start with a quadratic equation
ax2 + bx + c = 0.
(If a = 0, the equation wasn’t quadratic to begin with.)
Move the constant term to the other side:
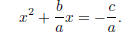
The idea is to add something to both sides to make the
left side a perfect square.
Represent the left side as the sum of the areas of a square (x2) and
a rectangle 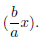 Divide the
Divide the
rectangle into two equal pieces.
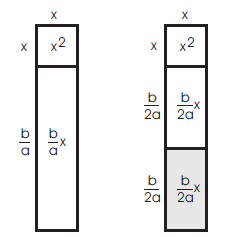
Move the bottom piece next to the square. The total area
is still the same. What is the area of the
square that must be added to “complete the square”?
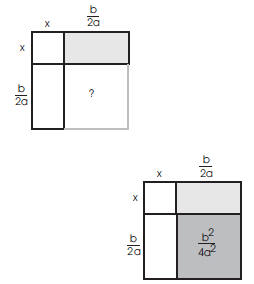
Since the missing square has sides of length b/2a , its
area is
b2/4a2 . This is what I need to add to both sides:
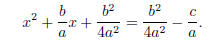
so
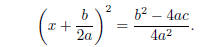
Take the square root of both sides and solve for x :
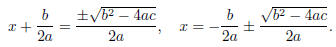
Theorem. (The Quadratic Formula) The solutions to ax2
+ bx + c = 0 are
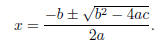
Example. Use the Quadratic Formula to solve x2
− 4x + 2 = 0.
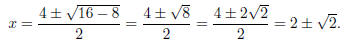
The roots are x = 2 + 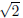 and x = 2 −
and x = 2 −
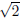 .
.
Example. Use the Quadratic Formula to solve 2x2 − 8x + 5 = 0.
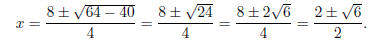
The roots are 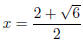 and
and
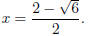
Example. Use the Quadratic Formula to solve x2 + 2x + 5 = 0.
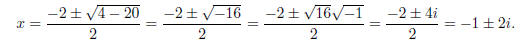
Example. Use the Quadratic Formula to solve x3 − 1 = 0.
x3 −1 = (x−1)(x2 +x+1), so x = 1 is
a root. To find the roots for x2 +x+1 = 0, I use the Quadratic
Formula:
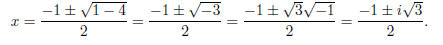
The roots are x = 1 and 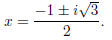
The Root Theorem says that if p(x) is a polynomial , then x
− c is a factor of p (x) if and only c is a
root of p(x).
To say that x−c is a factor of p(x) is the same as saying
that x−c divides p(x) (“evenly”). For example,
x − 3 divides x2 + 4x − 21, because
x2 + 4x − 21 = (x − 3)(x + 7).
Example. Factor 3x2 − 16x − 35.
By the Root Theorem, factoring is equivalent to finding roots. By the Quadratic
Formula, the roots are
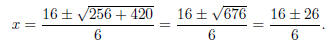
Now
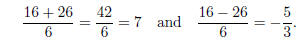
The root x = 7 corresponds to a factor x − 7; the root x =
−5/3
corresponds to a factor x +5/3. But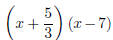 would have
x2 as its square term, whereas the original quadratic has 3x2.
Therefore, I have to multiply by 3 to get the correct factorization:
would have
x2 as its square term, whereas the original quadratic has 3x2.
Therefore, I have to multiply by 3 to get the correct factorization:
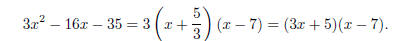
Example. Factor x2 − 6x + 6.
Factoring is equivalent to find the roots of x2 − 6x + 6 = 0.
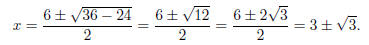
The roots are x = 3 + 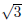 and x = 3 −
and x = 3 − 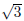 . This means that
. This means that
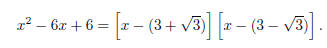
You can also use the Root Theorem to construct quadratics with given roots.
Example. Find a quadratic equation whose roots are 4 and −7.
c = 4 corresponds to the factor x−4. c = −7 corresponds to the factor x−(−7) = x+7. The quadratic
(x − 4)(x + 7) = x2 + 3x − 28
has roots 4 and −7.
Example. Find a quadratic equation whose roots are 2 −
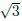 and 2 +
and 2 + 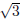 .
.
c = 2 − 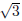 corresponds to the factor x − (2 −
corresponds to the factor x − (2 −
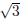 ). c = 2 +
). c = 2 + 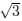 corresponds to the factor x − (2 +
corresponds to the factor x − (2 + 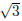 ).
).
The quadratic
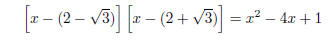
has roots 2 − 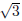 and 2 +
and 2 +
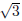 .
.
The term b2 − 4ac in the quadratic formula is
called the discriminant; it tells you about the roots of
the quadratic equation.
(a) If b2 − 4ac > 0, there are two (different) real roots.
(b) If b2 − 4ac = 0, there is one real root. (This is called a double
root or a repeated root.)
(c) If b2 − 4ac < 0, there are two complex roots. The complex roots
have the form p ± qi.
Example. For what value or values of k does
2x2 + kx + 5 = 0
have exactly one root?
The discriminant is
b2 − 4ac = k2 − 4(2)(5) = k2 − 40.
There is exactly one root when the discriminant is 0:
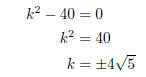
There is exactly one root when
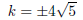 .
.
Example. Show that if k is any real number, the
equation
x2 − 4x + (5 + k2) = 0
has complex roots .
The discriminant is
b2 − 4ac = 16 − 4(5 + k2) = −4 − 4k2.
Since −4 − 4k2 is negative no matter what k is, the equation always
has complex roots.
| Prev | Next |