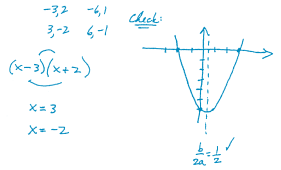The Myth of Objectivity in Mathematics Assessment

A wide array of alternatives to traditional
quiz-and-test assessment of students’ mathematical
understanding has been proposed
in the last decade (e.g., Stenmark [1991]; NCTM
[1995]; Greer et al. [1999]). Adding open -ended
problems, performance tasks, writing assignments,
and portfolios to teachers’ assessment repertoires is
important, these documents argue, because “assembling
evidence from a variety of sources is more
likely to yield an accurate picture of what each student
knows and is able to do” (NCTM 2000, p. 24).

The decision by teachers to incorporate some of
these less familiar assessment techniques is often
framed as a trade-off between objectivity and subjectivity.
Traditional assessment methods, which
are sometimes narrowly focused on skills and procedures,
are at least objective measures of those
skills and procedures. By contrast, alternative
approaches—which have the potential to assess
students’ conceptual understanding and their
problem- solving and reasoning ability—are unfortunately
subjective.

What does it mean for an assessment technique
to be objective? The American Heritage Dictionary
of the English Language defines the word as follows:

Ob•jec•tive adj. 1. Of or having to do with a material
object as distinguished from a mental concept, idea, or
belief. Compare subjective. 2. Having actual existence or
reality . 3. a. Uninfluenced by emotion, surmise, or personal
prejudice. b. Based on observable phenomena; presented
factually: an objective appraisal.

A student’s mathematical understanding —for
example, knowledge of linear functions or the
capacity to solve nonroutine problems—is a “mental
concept” and as such can be observed only indirectly.
Further, a teacher’s appraisal of this knowledge
cannot help but be influenced by emotion or surmise.

Objectivity, like the mythical pot of gold at the end
of the rainbow, would be wonderful if we could have
it, but it does not exist. All assessments of students’
mathematical understanding are subjective.

A more useful way to characterize methods of
assessment would be with respect to their consistency,
or reliability, and the meaning, or validity, of
the information that they provide. When different
teachers use a consistent method to assess the
knowledge of a given student, the teachers’ assessments
agree. When two students have roughly the
same level of understanding of a set of mathematical
ideas, consistent assessment of these students’
understandings is roughly equal, as well.

Meaningful methods give teachers information
about students’ understanding of specific mathematical
ideas and how this understanding changes
over time. This information can be used to make
appropriate instructional decisions.

The following examples of information collected
by using three familiar methods—a teacher-made
quiz, the Advanced Placement calculus test, and

Objectivity
would be
wonderful
if we could
have it,
but it does
not exist

the SAT-I Mathematics test—illustrate both the
inherent subjectivity of these methods and the
value of considering, instead, the consistency and
meaning of the methods.

A conclusion
about a
student’s
knowledge
would
require the
teacher’s
judgment

A TEACHER-MADE QUIZ

An algebra teacher who is hoping to assess students’
ability to solve quadratic equations might
include the following task on a quiz:

Solve: x² + x – 6 = 0.

Figure 1 shows one student’s response to this
task. Before reading any further, assess this second-year
algebra student ’s work and assign a point
value, assuming that “full credit” is five points and
that partial credit is allowed.

This student has correctly listed all factors of the
constant coefficient of the expression on the left
side of the equation. She used the first of these factor
pairs to construct two potential binomial factors
of the quadratic expression. She seems to have
checked the “outside” and “inside” products to
determine whether multiplying these binomials
produces a quadratic expression with the proper
middle term. Her first misstep is that the product
of these binomials does not produce the correct middle
term. She seems satisfied, though, and she proceeds
to write the solutions of the equation . Then,
in her “check,” she shows that a graph of the quadratic
function y = x² + x – 6 has x-intercepts at –2
and 3. Her graph, with its incorrect axis of symmetry,
confirms her answers.

What does this student know about solving quadratic
equations? She seems to know that one way
to solve them involves factoring the quadratic
expression. She also seems to know a method. She
knows the factors of –6. She might know that if a
product of two terms is zero , then at least one of the
terms is zero. She does know that the solutions of
this quadratic equation are specific points on the
graph of a quadratic function.

The teacher could conclude that this student
knows a great deal about solving quadratic equations
but has some trouble keeping signs straight ,
since both mistakes are sign errors. Or the teacher
could conclude that this student has tried to memorize
a procedure for solving quadratic equations
and has—perhaps without any understanding—
reproduced most, but not all, the steps correctly. A
conclusion about this student’s knowledge of quadratic
equations and how to solve them would
require the teacher’s judgment. This judgment
would have to be exercised in the face of incomplete
and ambiguous evidence furnished by the student
and without any explicit guidance.

What score did you assign to this paper? Why did
you assign that score? These questions have been
asked of practicing teachers in many classes, workshops,
and conference sessions in the last few years.
The responses have been distributed more or less
evenly among the scores 2, 3, and 4. This 40 percent
variation is attributable to judgments that
individual teachers made about the relative importance
of each aspect of this student’s work
described previously . In other words, these scores
are subjective.

Thus, an apparently straightforward question of
the most common and traditional type produced
assessment information that says as much about
the scorer as it does about the student. The scores
on quizzes and tests that consist of such items as
this example are inconsistent and may not offer
much information about the mathematical knowledge
of the student.