SOLVING SYSTEMS OF LINEAR EQUATIONS BY THE METHOD
Definitions:
• System of linear equations: consists of two or more linear equations with
the same variables.
•Consistent: The system is consistent if there is exactly one solution .
•Inconsistent: The system is inconsistent if there is no solution. This happens
when the two equations represent parallel lines.
•Dependent: The system is dependent if there is an infinite number of ordered
pairs as solutions.
This occurs when the two equations represent the same line.
Steps for the Method of Elimination :
1. Align the variables.
2. Multiply one or both equations by the appropriate constant so that the coe±cients
of one of the
variables are opposites of each other.
3. Add the two equations together. (If you have done everything correctly, this
will produce one equation
with one variable).
4. Solve the equation from Step 3.
5. Substitute the solution from Step 4 into either of the original equations.
This will give the value of
the other variable.
•If the equation in Step 3 above is a false statement (such as 7 = 2), then
the system is inconsistent.
•If the equation in Step 3 above is a true statement (such as 0 = 0), then the
system is dependent.
Common Mistakes to Avoid:
•Remember that a system of linear equations is not completely solved until
values for both x and y
are found. To avoid this mistake, write all answers as ordered pairs .
•Remember that all ordered pairs are stated with the x-variable first and the
y-variable second;
namely, (x; y).
1. Solve
6x - 5y = 25
4x + 15y = 13
If we multiply the first equation by 3 and
leave the second equation alone, we will eliminate y .
3(6x - 5y = 25)
4x + 15y = 13
We now have:
18x - 15y = 75
4x + 15y = 13
Adding these two equations together we get:
22x = 88
x = 4
Now, we must find the value for y by substituting x = 4 into one of the two original
equations. Substituting into the first equation gives
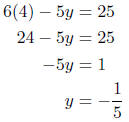
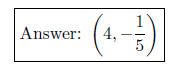
2. Solve
5x - 2y = 16
2x + y = 8
Multiplying the second equation by 2 will
eliminate the y variable.
5x - 2y = -16
2(2x + y = 8)
This gives us:
5x - 2y = -16
4x + 2y = 16
When we add these two equations together
we get:
9x = 0
x = 0
Now, we must find the value of y by substituting x = 0 into one of the two
original
equations. When we substitute x = 0 into the second equation, we get
2(0) + y = 8
y = 8
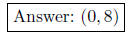
3. Solve
8x + 9y = 13
6x - 5y = 45
To eliminate the x variable we will multiply the first equation by -3 and the
second
equation by 4.
-3(8x + 9y = 13)
4(6x - 5y = 45)
This gives us:
-24x - 27y = -39
24x - 20y = 180
Adding these two equations together yields:
-47y = 141
y = -3
Next, we need to find the value for x by substituting y = -3 into either of the two original equations. If we substitute y = -3 into
the first equation, we get
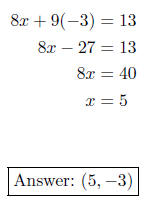
4. Solve
4x - 5y = 35
3x - 4y = 24
If we multiply the first equation by 3 and the
second equation by -4 we will eliminate the
x variable.
3(4x - 5y = 35)
-4(3x - 4y = 24)
This yields:
12x - 15y = 105
-12x + 16y = -96
When we add these two equations together,
we get:
y = 9
Next, to solve for the x variable we need to
substitute y = 9 into one of the two original equations. Substituting y = 9 into the
second equation, we get:
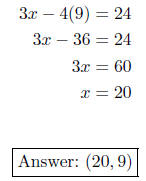
5. Solve
-6x + 9y = 12
2x - 3y = -4
If we multiply the second equation by 3 we
will eliminate the x variable.
-6x + 9y = 12
3(2x - 3y = -4)
This gives us:
-6x + 9y = 12
6x - 9y = -12
When we add these two equations together,
we get:
0 = 0
Since this is a true statement, we know that
the system is dependent. Therefore, there
are an infinite number of solutions.
Answer: dependent system
6. Solve
-5x + 4y = 1
15x - 12y = 4
If we multiply the first equation by 3 we will
eliminate the x variable.
3(-5x + 4y = 1)
15x - 12y = 4
This gives us:
-15x + 12y = 3
15x - 12y = 4
Adding these two equations together gives
us:
0 = 7
Since this is a false statement, we know that
the system is inconsistent. Therefore, there
is no solution.
Answer: No Solution
| Prev | Next |