Sixth Grade Math
A · Sixth Grade Math
In sixth grade, students are presented with different ways
to calculate the Least Common Multiple
( LCM ) and the Greatest Common Factor ( GCF ) of two integers. The LCM of two
integers a and b is
the smallest positive integer that is a multiple of both a and b. The
GCF of two
non-zero integers a
and b is the largest positive integer that divides both a and b
without
remainder.
For this problem you will write a program that determines both the LCM and
GCF
for positive
integers.
Input
The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the
number of data sets that
follow. Each data set consists of a single line of input containing two positive
integers, a and b,
(1 ≤ a, b ≤ 1000) separated by a space.
Output
For each data set, you should generate one line of output with the following
values: The data set
number as a decimal integer (start counting at one), a space, the LCM, a space,
and the GCF.
| Sample Input | Sample Output |
 |
|
B · Cryptoquote
A cryptoquote is a simple encoded message where one letter is simply replaced by
another
throughout the message. For example:
Encoded: HPC PJVYMIY
Decoded: ACM CONTEST
In the example above, H=A, P=C, C=M, J=O, V=N, Y=T, M=E and I=S. For this
problem, you will
decode messages.
Input
The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the
number of data sets that
follow. Each data set consists of two lines of input. The first line is the
encoded message. The
second line is a 26 character string of upper case letters giving the character
mapping for each letter
of the alphabet: the first character gives the mapping for A, the second for
B
and so on. Only upper
case letters will be used. Spaces may appear in the encoded message, and should
be preserved in
the output string.
Output
For each data set, you should generate one line of output with the following
values: The data set
number as a decimal integer (start counting at one), a space and the decoded
message.
| Sample Input | Sample Output |
| 2 HPC PJVYMIY BLMRGJIASOPZEFDCKWYHUNXQTV FDY GAI BG UKMY KIMHOTSQYRLCUZPAGWJNBVDXEF |
1 ACM CONTEST 2 THE SKY IS BLUE |
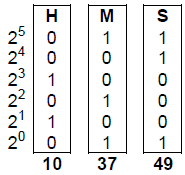
C · Binary Clock
A binary clock is a clock which displays traditional sexagesimal time (military
format) in a binary
format. The most common binary clock uses three columns or three rows of LEDs to
represent zeros
and ones. Each column (or row) represents a time-unit value.
When three columns are used (vertically), the bottom row in each column
represents 1 (or 20), with
each row above representing higher powers of two, up to 25 (or
32). To read each
individual unit
(hours, minutes or seconds) in the time, the user adds the values that each
illuminated LED
represents, and then reads the time from left to right. The first column
represents the hour, the next
column represents the minute, and the last column represents the second.
When three rows are used (horizontally), the right column in each row represents
1 (or 20), with each
column left representing higher powers of two, up to 25 (or 32). To read each
individual unit (hours,
minutes or seconds) in the time, the user adds the values that each illuminated
LED represents, and
then reads the time from top to bottom. The top row represents the hour, the
next row represents the
minute, and the bottom row represents the second.
For example:
| 0 = LED off Vertically |
1 = LED on Horizontally |
 |
 |
Time is: 10 : 37 : 49
For this problem you will read a time in sexagesimal time format, and output
both the vertical and
horizontal binary clock values. The output will be formed by concatenating
together the bits in each
column (or row) to form two 18 character strings of 1’s and 0’s as shown below.
10:37:49 would be written vertically as 011001100010100011
and horizontally as
001010100101110001.
Input
The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the
number of data sets that
follow. Each data set consists of a single line of input containing the time in
sexagesimal format.
Output
For each data set, you should generate one line of output with the following
values: The data set
number as a decimal integer (start counting at one), a space, the binary time in
vertical format (18
binary digits ), a space and the binary time in horizontal format (18 binary
digits).
| Sample Input | Sample Output |
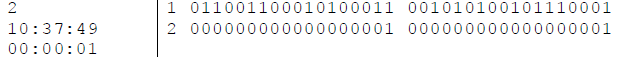 |
|
D · Recursively Palindromic Partitions
A partition of a positive integer N is a sequence of integers which sum to N,
usually written with plus
signs between the numbers of the partition. For example
15 = 1+2+3+4+5 = 1+2+1+7+1+2+1
A partition is palindromic if it reads the same forward and backward. The first
partition in the example
is not palindromic while the second is. If a partition containing m integers is
palindromic, its left half is
the first floor(m/2) integers and its right half is the last floor(m/2) integers
(which must be the
reverse of the left half. (floor(x) is the greatest integer less than or equal
to x.)
A partition is recursively palindromic if it is palindromic and its left half is
recursively palindromic or
empty. Note that every integer has at least two recursively palindromic
partitions one consisting of all
ones and a second consisting of the integer itself. The second example above is
also recursively
palindromic.
For example, the recursively palindromic partitions of 7 are:
7, 1+5+1, 2+3+2, 1+1+3+1+1, 3+1+3, 1+1+1+1+1+1+1
Write a program which takes as input an integer N and outputs the number of
recursively palindromic
partitions of N.
Input
The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the
number of data sets that
follow. Each data set consists of a single line of input containing a single
positive integer for which
the number of recursively palindromic partitions is to be found.
Output
For each data set, you should generate one line of output with the following
values: The data set
number as a decimal integer (start counting at one), a space and the number of
recursively
palindromic partitions of the input value.
| Sample Input | Sample Output |
 |
|
| Prev | Next |