Pre Calculus Midterm Exam 2 - Solutions
1. (10 points) Suppose that f(x) = 2x + 1 and g(x) = -x +
4.
(a) (4 points) Solve f (x) = g(x).
Solution: We have 2x + 1 = -x + 4 thus 3x = 3 and x = 1.
(b) (4 points) Solve f(x) < g(x)
Solution: We have 2x + 1 < -x + 4 thus 3x < 3 and x < 1.
(c) (2 points) What is the geometric interpretation of f(x) = g(x)?
Solution: f(x) and g(x) are both linear functions and their graphs are
straight lines.
The solution of f(x) = g(x) is the x-coordinate of the point of intersection of
these two
lines .
2. (20 points) Find a quadratic function whose graph is a parabola with vertex
at the
point (2,3) and whose y-intercept has the y-coordinate equal 11.
Solution: Since we are given the coordinates of the vertex we know that
the function
will have the form
f(x) = a(x - 2)2 + 3
for some a 2 R. Now, using the y-intercept we get that 11 = a(0 - 2)2 + 3 thus a
= 2.
3. (20 points) Consider the polynomial
P(x) = (x + 2)2(x - 1)(x - 2)3
(a) (3 points) List zeros of P (x) with their multiplicities.
Solution: We have x = -2 with multiplicity 2, x = 1 with multiplicity 1
and x = 2
with multiplicity 3.
(b) (3 points) Determine whether the graph crosses or touches the x-axis at each
x-intercept.
Solution: The graph touches the x-axis at x = -2 (since the multiplicity
is even) and
crosses it at x = 1 and x = 3 (since multiplicities are odd ).
(c) (10 points) Determine the behaviour of th graph near each x-intercept.
Solution: The polynomial P(x) is already factored. We get
At x = -2 we have 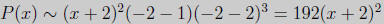
At x = 1 we have 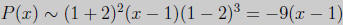
At x = 2 we have 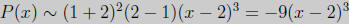
(d) (4 points) Determine the end behaviour, that is, find
the power function that
the graph resembles for large values of 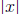 .
.
Solution: The leading term in P(x) is x6 thus the power function we are
looking for is
f(x) = x6 .
4. (30 points) Consider the functions
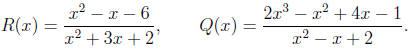
(a) (5 points) Find the vertical asymptotes of R(x).
Solution: The domain of R(x) is all real x except if x2 + 3x + 2 = 0.
Thus we have
two candidates for vertical asymptotes, x = -1 and x = -2. Factoring the
numerator
and denominator we have
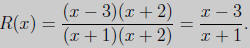
The last formula is R (x) in lowest terms . Thus the only vertical asymptote is x
= -1.
(b) (12 points) Find the horizontal and oblique asymptotes of R(x), if any.
Solution: Using long division we find that
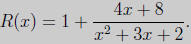
In the second term the degree of the numerator is strictly less than the degree
of the
denominator hence as  we have
we have
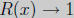 . y = 1 is a horizontal asymptote.
. y = 1 is a horizontal asymptote.
(c) (12 points) Find the horizontal and oblique asymptotes of Q(x), if any.
Solution: Using long division we find that
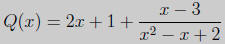
Again, in the third term the degree of the numerator is strictly less than the
degree of
the denominator hence as 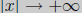 this term goes to
zero. y = 2x + 1 is an oblique
this term goes to
zero. y = 2x + 1 is an oblique
asymptote of Q(x)
(d) (1 point) Can a rational function have a horizontal asymptote and an oblique
asymptote at the same time? Justify your answer.
Solution: Every horizontal asymptote is an oblique asymptote so if a
function has a
horizontal asymptote it also has an oblique one. If a function has a
non-horizontal
oblique asymptote it cannot have another horizontal asymptote at the same time.
5. (20 points) A wire 20 meters long is to be cut into two
pieces. Both pieces will be
shaped as a square. Express the total area A enclosed by the pieces of wire as a
function of length x of a side of one of the squares. What is the domain of A?
What
is the minimal value of A? What is the maximal physically possible value of A?
Solution: Let the first piece have lenght 4x. The remaining part has then
length
20-4x. Since both pieces are bent to squares the first one has sides with length
x, the
second one with length 5 - x. The sum of areas of both squares is

Despite A(x) is well defined for all real x there are some restrictions i.e. 0 <
x < 5.
This is the domain of A(x). Now, notice that A(x) is a quadratic function whose
graph
is a parabola that opens up hence the minimal value is attained at the vertex.
The
x-coordinate of the vertex is h = 2.5 and this is actually the length of the
side of both
squares in this case.
Extra Credit
6. (20 points) Inscribe a right circular cylinder of height h and radius r in a
sphere of
fixed radius R (see illustration). Express the volume V of the cylinder as a
function
of h (only). (Hint: the volume of a cylinder with radius r and height h is
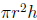 .
Note
.
Note
also the right triangle.)
Solution: Let r be the radius of the base of the cylinder and h its
height. Then the
formula for the volume of a cylinder yields 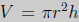 .
This quantity depends on two
.
This quantity depends on two
variables -h and r. We have to get rid of r. We use the right triangle with
sides r, h/2 and
R and from the Pythagorean theorem we get  .
Thus
.
Thus 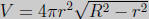 .
.
| Prev | Next |